Inscription / Connexion Nouveau Sujet
probleme
pouvez vous m'aider avec ce probleme svp je bloque depuis qqs jours.
On se donne un cercle C de rayon 1. On cherche les triangles ds C qui ont une aire maximale.
a) Montrer que si XYZ est un triangle non isocele inscrit ds C alors il existe X'Y'Z' isocele inscrit ds C dont l'aire est strictement plus grande que celle de XYZ
b) Si X'Y'Z' est un triangle isocele en X' inscrit ds C et d'angle en X' egal a theta, calculer la base et la hauteur de ce triangle et en deduire une formule pour l'aire A ( theta) de ce triangle en fonction de theta
c) montrer que A (theta) est maximale pour theta = pi/3
Voila : ), merci !
Nadia
Bonsoir 
Alors, voici quelques petites formules qui peuvent t'aider.
(sans démonstration...)
Soit S l'aire d'un triangle ABC (inscrit dans un cercle en l'occurence, dans un cercle de rayon R, on appelle p le demi périmètre du triangle ABC, soit p = (a+b+c)/2), BC = a, CA = b, AB = c.
ha la hauteur issue de A.
S = (a*ha)/2 (la plus connue de toutes)
S = (a*b*sin(B))/2 (une petite consequence de la précédente
S = (a*b*c)/(4*R)
En définissant un cercle inscrit, on a:
S = p*r , avec r = rayon du cercle inscrit.
Et une petite dernière, un peu plus subtile :
(Il s'asit de la formule d'Heron)
Voila, avec ces petites egalités, je pense que tu vas pouvoir avancer dans ton devoir.
A bientot
Ghostux

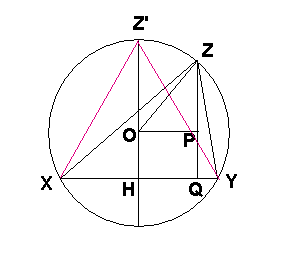
Une possibilité pour le point a.
Soit le triangle non isocèle XYZ inscrit dans le cercle de centre O.
Tracer HZ' médiatrice de [XY] (voir dessin.)
Remarque: la droite(HZ') passe par O comme médiatrice d'une corde du cercle.
Soit Q le pied de la hauteur issue de Z du triangle XYZ.
La droite HOZ' est // à la droite ZQ (car elles sont toutes 2 perpendiculaires à la droite XY).
Tracer OP // à XY (voir dessin)
On a OH = PQ (cotés opposés du rectangles OPQH)
Dans le triangle rectangle OPZ, PZ est plus petit que OZ (un coté de l'angle droit d'un triangle rectangle est toujours plus petit que l'hypoténuse).
Or OZ = OZ' commes rayons du même cercle.
-> OZ' > PZ (1)
Z'H = OH+OZ'
Z'H = PQ + OZ' (2)
ZQ = PQ + PZ (3)
(1), (2) et (3) ->
Z'H > ZQ (4)
Aire(XYZ) = (1/2).XY.ZQ
Aire(XYZ') = (1/2).XY.Z'H
Les 2 lignes précédentes avec (4) ->
Aire(XYZ') > Aire(XYZ)
Donc en prenant X' confondu avec X et Y' confondu avec Y, on a :
Aire(X'Y'Z') > Aire(XYZ)
Comme Z'H est médiatrice de [XY], on a XZ' = Z'Y et donc le triangle XYZ' (ou X'Y'Z') est isocèle.
On a donc montré qu'il existe un triangle(X'Y'Z') isocèle dont l'aire est supérieure à celle du triangle XYZ.
-----
Sauf distraction. 
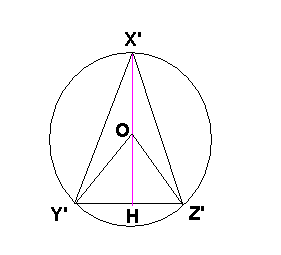
Pour la partie b.
X'H est la hauteur issue de X' du triangle X'Y'Z', mais X'H est aussi médiatrice de [Y'Z'] -> |HZ'| = (1/2).|Y'Z'|
angle(Y'X'Z') = (1/2).angle(Y'OZ')
angle(HOZ') = (1/2).angle((Y'OZ')
-> angle(HOZ') = angle(Y'X'Z')
angle(HOZ') = Theta.
-----
OH = OZ'.cos(HOZ')
OH = R.cos(theta) (Avec R le rayon du cercle).
X'H = R + OH
X'H = R(1+cos(theta))
HZ' = OZ'.sin(HOZ')
HZ' = R.sin(Theta)
Y'Z' = 2R.sin(Theta)
Aire(X'Y'Z') = (1/2).Y'Z'.X'H
Aire(X'Y'Z') = (1/2).2R.sin(Theta).R(1+cos(theta))
Aire(X'Y'Z') = R².sin(Theta).(1+cos(theta))
-----
A(Theta) = R².sin(Theta).(1+cos(theta))
Reste à montrer que A(Theta) est max pour theta = Pi/3.
Soit une étude simple de fonction.
...
-----
Sauf distraction. 
Bonjour, merci pour votre aide,
mais je me pose la question, pourquoi :
angle(Y'X'Z') = (1/2).angle(Y'OZ') ??
Merci
angle(Y'X'Z') = (1/2).angle(Y'OZ')
Un angle au centre sous-tendant une corde d'un cercle a une mesure double d'un angle sous-tendant la même corde et qui a son sommet sur le cercle (à la condition que le sommet de l'angle et le centre du cercle soient du même coté de la corde).
Pour le démontrer:
OX' = OZ' comme rayons d'un même cercle.
-> le triangles X'OZ' est isocèle en O
-> angle(OX'Z') = angle(OZ'X')
La somme des angles d'un triangle = 180°->
dans le triangle OX'Y': angle(OX'Z') + angle(OZ'X') + angle(X'OZ') = 180°
2.angle(OX'Z') + angle(X'OZ') = 180°
angle(X'OZ') = 180° - 2.angle(OX'Z') (1)
Voir dessin: angle(HOZ') = 180° - angle(X'OZ')
angle(HOZ') = 180° - (180° - 2.angle(OX'Z'))
angle(HOZ') = 2.angle(OX'Z')
(1/2).angle(Y'OZ') = angle(Y'X'Z')
Et voila. 


 géométrie en post-bac
géométrie en post-bac