Inscription / Connexion Nouveau Sujet
Problème 2
Bonjour,
Pouvez-vous m'aider à résoudre ce problème, je ne vois pas comment commencer...
Soit ABCD un carré de côté quelconque. On construit deux triangles équilatéraux ABF et ADE comme sur la figure. Le triangle EFC est-il équilatérale?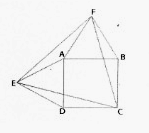
***malou > image un peu améliorée***
Réponse : oui.
Pour le prouver, tu pourrais essayer de montrer que les triangles CBF, FAE et EDC sont des triangles isocèles égaux.
Merci pour votre réponse,
ABCD est un carré donc AB = BC = CD = DA
ABF est un triangle équilatéral donc AB = BF = FA or AB = BC donc BC = BF => CBF est un triangle isocèle en B
ADE est un triangle équilatéral donc AD = DE = EA or AD = CD donc CD = DE => EDC est un triangle isocèle en D
ABF est un triangle équilatéral donc AB = BF = FA
ADE est un triangle équilatéral donc AD = DE = EA
Comme AB = AD (carré) on a FA = EA => FAE est un triangle isocèle en A
CBF, FAE et EDC sont des triangles isocèles égaux donc EFC est équilatéral.
Est-ce que c'est suffisant pour conclure que le triangle est équilatéral?
Merci 
Non, cela ne suffit pas. Il faut encore démontrer que ces trois triangles isocèles sont égaux. Pour cela, raisonne sur les angles.
Merci,
CBF est un triangle isocèle en B => angle (F) = angle (C)
EDC est un triangle isocèle en D => angle (E) = angle (C)
FAE est un triangle isocèle en A => angle (E) = angle (F)
Finalement angle (E) = angle (F) = angle (C) mais est-ce que c'est suffisant?


