Inscription / Connexion Nouveau Sujet
Problème
Mon fils se trouve face à un problème à résoudre
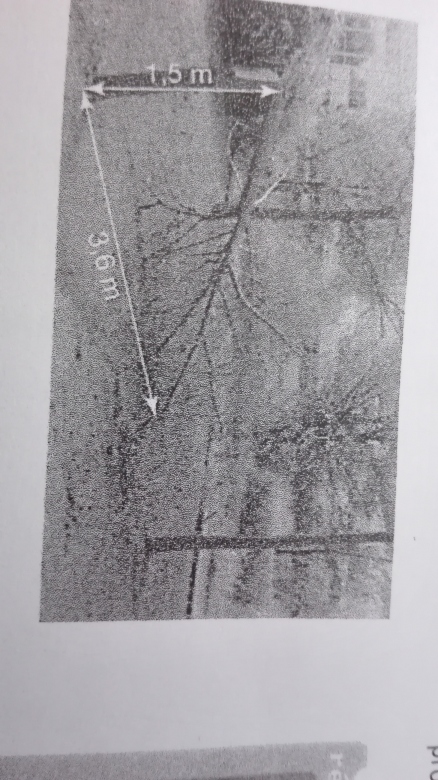
Un arbre de 5,4 m de haut planté sur un sol horizontal à été brisé. Son sommet est désormais sur le sol à 3,6 m de son pied.
1)Calculer la longueur de la partie superieure de l'arbre, de la cassure au sommet.
2)La partie inférieur de l'arbre est-elle restée verticale ? le démontrer
tout ce que tu vois d'affiché sur le site on le voit
pour être sur il est conseillé (fortement) de faire Aperçu (le bouton Aperçu) avant de poster.
en particulier pour vérifier que sa photo est dans le bon sens (sinon, à l'avenir, la refaire)
je l'ai tournée et rajouté des noms de points :

1)Calculer la longueur de la partie supérieure de l'arbre, de la cassure au sommet.
bein s'il en reste 1.5m et que sa hauteur initiale était de 5,4 m c'est assez évident !! (quel que soit l'endroit où tombe la partie supérieure)
2) Pythagore, la partie supérieure étant BC calculée question 1.
merci pour l'information d'utilisation,
donc 5.4 -1.5 =3.9 m
et ensuite il faut appliquer le théorème de Pythagore ab²+ac²=bc²
Bonjour, excusez moi de vous déranger à nouveau, voilà le résultat que mon fils me donne Soit ABC est un triangle en B tels que AB=1.5 et que AC=3.9 Calculer BC. Dans le triangle ABC rectangle en B l'hypoténuse est AC, AB=1.5m et AC=3.9m ; D'après le théorème de Pythagore, AC²=AB²=BC²
3.9²=1.5²=BC²
15.21=2.25=BC²
BC²=12.96
BC²=√12.96
BC²=3.6
Et en réponse à la question 2, oui elle est restée verticale. il doit faire une démonstration pour prouver que la partie inférieur de l'arbre est restée verticale...
ça c'est pour la question 2
la question 1 c'est uniquement la différence 5.4 -1.5 =3.9 m et rien d'autre
on ne sait pas du tout si le triangle est rectangle ou pas !!
question 2 :
Dans le triangle ABC rectangle en B ... faux et de plus on n'en sait rien du tout !!
la base du raisonnement est dés le départ fausse
on ne sait pas du tout si le triangle est rectangle ou pas !!
c'est ce qu'on demande de prouver, ou de prouver qu'il ne l'est pas
il faut utiliser la réciproque du théorème de Pythagore :
si dans un triangle ABC de plus grand côté BC (c'est bien le cas BC = 3,9 est > 3,6 et > 1.5)
on a BC² = AB² + AC² alors ce triangle est rectangle en A
donc on calcule séparément AB² + AC²
et BC²
et si les deux sont égaux, alors le triangle sera rectangle en A et la souche verticale (perpendiculaire au sol horizontal)
et sinon non.
Soit ABC est un triangle tels que AB=1.5m; BC=3.9m et AC=3.6. Le triangle ABC est-il rectangle?
Dans le triangle ABC, le plus grand coté est BC, on a d'une part
BC²=3.9²
BC²=15.21
et de l'autre part,
AB²+AC²=1.5²+3.6²=2.25+12.96=15.21
donc, BC²=AB²+AC² d'après la réciproque du théorème, le triangle ABC est rectangle en A et l'hypoténuse est BC
La souche est donc restée verticale
Ce raisonnement est-il juste??