Inscription / Connexion Nouveau Sujet
Probleme avec angle orienté
Bonjour j'ai un probleme a faire pendant les vacances j'avoue qu'il est assez difficile vu que le cours sur les angles nous l'avons survolé cause des greves.
Donc la prof nous donne un probleme ou je n'ai vraiment pas compris grand chose je vous demande de l'aide .
Merci d'avance
Voici le sujet
Pentagone régulier lignes trigonometrique de 2 //5
//5
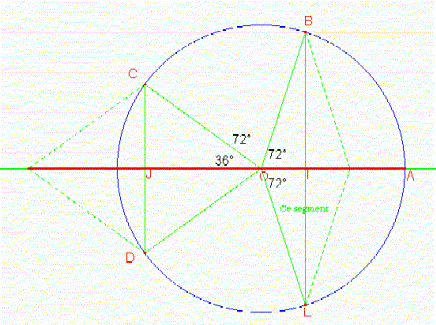
ABCDE est un pentagone régulier direct inscrit dans le cercle trigonometrique C de centre O.
1) Indiquer les mesures des angles orientés (OA OB) (OA OC) (OA OD) (OA OE)
b) Exprimer OB+OE et OC+OD en fonction du vecteur OA
2)a) On appelle l'isobarycentre des points A, B, C, D, E.
l'isobarycentre des points A, B, C, D, E.
Demontrer que O est barycentre des points pondéres
( ;-5) et (A, 1+2cos2
;-5) et (A, 1+2cos2 /5+2cos4
/5+2cos4 //5)
//5)
b) On considère la rotation de centre O et d'angle 2 /5
/5
Comment transforme t-elle le pentagone ABCDE ?
En déduire que  ,O et B sont alignés.
,O et B sont alignés.
c) Que peut on en conclure pour le point et pour:
et pour:
1+2cos2 //5+2cos 4
//5+2cos 4 //5
//5
3)a) Resoudre l'equation 4x²+2x-1=0 dans 
b) Demontrer que cos 2 //5 est solution de cette equation.
//5 est solution de cette equation.
c) En deduire la valeur exacte de cos2 //5 ainsi que celle de sin2
//5 ainsi que celle de sin2 //5
//5
Voila en esperant de l'aide
L'angle au centre d'un pentagone vaut 2 comm il est régulier Chaque angle (OA;OB); (OB,OC)....vaut 2
comm il est régulier Chaque angle (OA;OB); (OB,OC)....vaut 2 /5 donc (OA,OB)=2
/5 donc (OA,OB)=2 /5; TU peux ainsi calculer les aures angles
/5; TU peux ainsi calculer les aures angles
merci de m'avoir répondu peut tu m'aider a continuer c'est surtout la suite qui me gène le plus.
Je n'arrive pas a faire une figure qui corresponde a ce qui me demande.
J'aurais besoin d'aide probleme assez difficile a resoudre.
merci par avance
Bonjour
1b)OA est un axe de symétrie (OB,OC,OD,OE aussi) pour le pentagone
I = BE inter OA et OB+OE = 2OI = 2.cos(72°)OA (|OA|=1)
J = CD inter OA et OC+OD = 2OJ = 2.cos(144°)OA = -2cos(36°)OA
*
2)a)soit M= on a MA+MB+MC+MD+ME=0 => 5MO+OA+OB+OC+OD+OE=0 => -5OM + OA +2cos(72°)OA +2cos(144°)OA = 0 => -5OM + (1+2cos(72°)+2cos(144°)OA = 0 => O,M et A sont alignés
on a MA+MB+MC+MD+ME=0 => 5MO+OA+OB+OC+OD+OE=0 => -5OM + OA +2cos(72°)OA +2cos(144°)OA = 0 => -5OM + (1+2cos(72°)+2cos(144°)OA = 0 => O,M et A sont alignés
b) vu la symétrie on aurait O, M et B sont alignés ou par la rotation qui transforme le pentagone en lui-même.
on aurait de même O,M et C alignés => M= =O =>
=O =>
OA+OB+OC+OD+OE=0 => OA+2OI+2OJ = 0 => |OA|+2|OI|-2|OJ| = 0 =>
c) 1 + 2cos(72°)- 2cos(36°)= 0 ou 1 + 2cos(72°) + 2cos(144°) = 0
*
3)a)la racine positive de 4x² + 2x -1 =0 est (rac(5) - 1)/4
b)comme cos(144°)= 2.cos²(72°)-1 par le 2b)on a 4cos²(72°) + 2cos(72°) -1 =0 donc sol. de 3)a)
c) => cos(72°) = {rac(5)-1}/4 => sin(72°)= rac{ 1 -cos²(72°)} = ....
à+ geo3
Bonjour geo3 et un grand merci pour ton aide mais je n'ai pas bien compris ton résonnement surtout les cos(72°)cos(144) c quoi tous ces chiffres d'ou sortent ils.
Merci je vous demande une autre explication un peu moin rappide que celle ci car a vrai je n'ai pas tout suivi et tout compris pouvez m'expliquer étape par étape j'espere ne pas vous déranger.
Un grand merci.
Rebonjour
1)L'angle au centre d'un pentagone est 360°/5 = 72° ou 2pi/5
Dans le triangle OBI rectangle en avec OB = 1 OI = cos(72°) = la demi-diagonale du parallélogramme construit sur OB et OE ;regardes la figure
*
2)a) définition du barycentre le reste c'est Chasles et le1)
2b)cos(144°) = -cos(36°)
OA+OB+OC+OD+OE = 0 car M= =O
=O
pour le reste je ne peux rien dire de plus
3)cos(144°)= 2.cos²(72°)-1 c'est une formule
à+
Bonjour geo3 je vais t'embeter encore un tout petit peu voila dans la question 2)b) on doit démontrer que  O et B sont alignés mais toi tu démontre que O,M et C sont alignés je n'ai pas compris t'es tu trompé?
O et B sont alignés mais toi tu démontre que O,M et C sont alignés je n'ai pas compris t'es tu trompé?
Ensuite tu trouve (rac(5) - 1)/4 moi je trouve (rac(5) - 2)/4 et ensuite tu dis que cos(72°) = {rac(5)-1}/4
quand je calcule a la calculatrice je ne trouve pas que c'est égale.
Voila si tu peut m'expliquer ce passage sinon tout le reste j'ai réussi grace a ton aide
Excuse moi je me suis trompé je trouve bien cos(72°) = {rac(5)-1}/4 mais je n'arrive pas a trouver 4x² + 2x -1 =0 est (rac(5) - 1)/4
j'ai beau recommencé 20 fois je ne trouve pas.
Bonjour
2a)En fait je t'ai informé que M=
donc d'abord c'est  ,O et A qui sont alignés
,O et A qui sont alignés
*
b)ensuite par la rotation de centre O et d'angle 2pi/5 le pentagone ABCDE est transformé en BCDEA et en recommençant ce qui a été fait au a) on peut dire que  ,O et B sont alignés
,O et B sont alignés
on pourrait continuer et dire que  ,O et C sont alignés et donc
,O et C sont alignés et donc  =O
=O
*La formule pour les racines d'une équation du second dégré ax²+bx+c=0 est
{ -b
 (b²-4ac)}/(2a)
(b²-4ac)}/(2a)
pour 4x²+2x-1 = 0 on a pour la racine positive = {-2+ (4+16)}/8 ....
(4+16)}/8 ....
à+
rebonjour voila j'espere pas trop t'embeter avec mes question mais il y a un point que je ne comprend pas comment passe tu -5OM + (1+2cos(72°)+2cos(144°)OA = 0
puis dire ensuite que O,M et A sont aligné je ne vois pas le rapport.
Rebonsoir
Regardes 2a) du 11 à 21h28
Quel est la définition du barycentre G est barycentre de (A,a) et (B,b) ssi
aGA+bGB=0 et G,A,B sont alignés car GA est multiple de GB ( cond. a+b doit différé de 0)
*
O est le barycentre de M et A, M affecté du poids -5 et affecté du coéfficient de OA c-à-d (1+2cos(72°)+2cos(144°)) et lorsque OM = 1 multiple de OA tu dois savoir que O,M et A sont alignés.
à+
Ok merci merci beaucoup une toute petite question encore puis je retrouver cette formulle grace a mes resultats sinnon le prof va me demander d'ou sort cette formule qui est celle ci cos(144°)= 2.cos²(72°)-1
Bonsoir
à partir du cos d'une somme cos(a+b) = cos(a)cos(b) - sin(a)sin(b)
cos(144°) = cos(72°+72°) = cos(72°).cos(72°) - sin(72°).sin(72°) = cos²(72°) - sin²(72°) =
cos²(72°) - ( 1 - cos²(72°)) = 2cos²(72°) - 1
A plus
Je suis désolée mais je ne sais pas comment on fait pour trouver le poste 76734.
Si vous pouvez m'aider...
Merci d'avance
*** message déplacé ***
blum >> Que veux-tu ?
Je ne comprends pas ta question. Peux-tu être plus clair(e) ?

*** message déplacé ***
Je cherche une aide pour exercie qui est déjà été posté sur le site. Mais la personne qui a répondu au probleme, nous renvoi au poste 76734.
Je vous passe le topic:
https://www.ilemaths.net/sujet-duplication-second-degre-pentagone-77750.html
*** message déplacé ***
Tout simplement comme ceci : 
![]() Probleme avec angle orienté
Probleme avec angle orienté
Vas-y vite ; je vais effacer tout cela !

*** message déplacé ***


