Inscription / Connexion Nouveau Sujet
Problème d équation différentielle
Pourriez vous m'aider a résoudre se problème. Meme si c'est que quelleque piste. Merci d'avances.
Lorsqu'une personne absorbe à jeun une quantité d'alcool, on note f(t) le taux d'alcoolémie ( g/L) à l'instant t (en heure) de son organisme. on considère que f est définie par l'équation différentielle: f'(t)=a e^-t-f(t) et f(0)=0. ( a est une constante positive dépendant de la personne et de la quantité d'alcool absorbée).
1) On pose g(t)=etf(t). Calculer g'(t) et en decuire que g est une fonction affine.
2) Exprimer f(t) en fonction de a et de t.
3) On suppose dans la suite que a =5.
a) Déterminer le taux d'alcoolémie maximal et le temps au bout duquel ce taux est atteint.
b) Etudier sur [0;+
[ la fonction f et dresser le tableau de variation.
Tracer la représentation graphique C de f dans un repère orthogonal du plan.
c) Au bout de combien de teps la personne peut-elle prendre le volant sans enfreindre la législation ? ( le taux autorisé est 0.5g/l).
1)
g(t) = e^t . f(t)
g'(t) = e^t.f(t) + e^t.f'(t)
g'(t) = e^t.f(t) + e^t.(a.e^-t - f(t))
g'(t) =a. e^t .e^-t
g '(t) = a
et donc g(t) = at + b
g est une fonction affine.
-----
2)
f(t) = g(t)/e^t
f(t) = at.e^-t + b.e^-t
Comme f(0) = 0 -> b = 0
f(t) = at.e^-t
-----
3)
a et b)
f(t) = 5t.e^-t
f '(t) = 5.e^-t - 5t.e^-t
f '(t) = 5.e^-t .(1-t)
f '(t) > 0 pour t dans [0 ; 1[ -> f(t) est croissante.
f '(t) = 0 pour t = 0.
f '(t) < 0 pour t dans ]1 ; oo[ -> f(t) est décroissante.
f(t) est maximum pour t = 1
Ce max vaut f(1) = 5*1*e^-1 = 5/e = 1,84
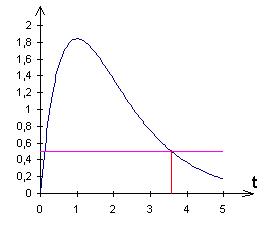
Le taux d'alcoolémie max est de 1,84 et il est atteint pour t = 1 heure.
---
c)
On lit sur le graphique t >= 3,6 heures.
---
Sauf distraction. 
Annuler
connectez vous