Inscription / Connexion Nouveau Sujet
Problème de 1e S : Equation de droites et de cercles
Bonjour à tous,
J'ai actuellement un DNS de Mathématiques à réaliser.
L'un des exercices de ce DNS porte sur un problème alliant équations de droites et de cercles.
En voici l'énoncé :
Le plan est muni d'un repère orthonormé (O; ;
; )
)
Soit C d'équation : x2+y2-6x-2y-15 = 0 et D la droite d'équation : 4x+3y = 0.
1. a. Démontrer que C est un cercle dont on déterminera le centre I et le rayon r.
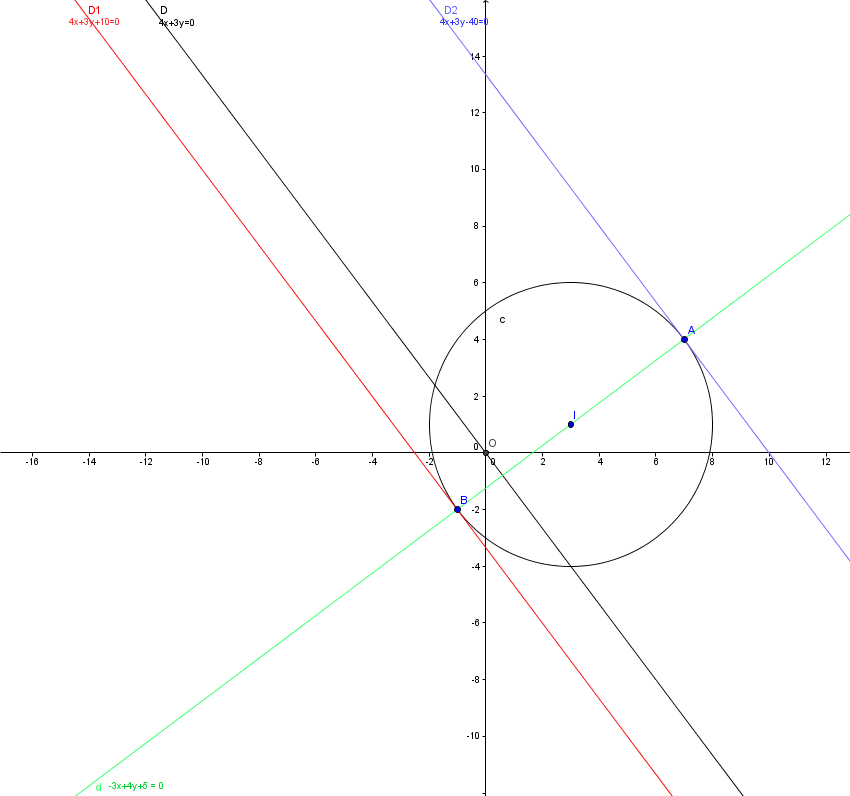
b. Construire le cercle C et la droite D.
c. Construire, en justifiant, les droites D1 et D2 tangentes à C et parallèles à D.
2. a. Déterminer une équation cartésienne de la droite (d) passant par I et perpendiculaire à D.
b. Déterminer les coordonnées des points A et B d'intersection de (d) avec C.
(pour la suite, on pourra admettre que A (7 ; 4) et B (-1 ; -2)
c. En déduire une équation cartésienne de chacune des droites D1 et D2.
3. a. Calculer la distance du point A à la droite D, et du point B à la droite D.
b. En déduire la distance entre D1 et D, et entre D2 et D.
Bonsoir
comme promis premiers éléments de répônse :
Q1a : l'équation d'un cercle (C) est du type x²+y²+ax+by+c=0 avec ici a=-6, b=-2, c=-15.
On examine le nombre N = a²+b²-4c, soit 36+4+60 = 100
N>0, dc (C) est l'équation du cercle de centre I (-a/2;-b/2), soit I (3;1) et de rayon R=( R)/2, soit R = 5.
R)/2, soit R = 5.
Q1b : voir schéma
Q1c : (D1) et (D2) sont resp. de la forme 4x+3y+m=0 et 4x+3y+n=0, puisque  à (D). Comme ces droites sont tangentes à (C), la distance qui sépare le point de tangence (de contact) de I est égale à R, puisque chq rayon d'un cercle est porté par une droite perpendiculaire à la tangente au cercle passant par le point d'intersection de ce rayon avec le cercle.
à (D). Comme ces droites sont tangentes à (C), la distance qui sépare le point de tangence (de contact) de I est égale à R, puisque chq rayon d'un cercle est porté par une droite perpendiculaire à la tangente au cercle passant par le point d'intersection de ce rayon avec le cercle.
Et ds le plan muni d'un repère orthonormé, la distance d d'un point de coordonnées (x;y) à une droite d'équation ax+by+c=0 est donnée par la formule
On connaît a,b,R, x et y, on va dc pouvoir déterminer c et trouver les équations cartésiennes complètes de (D1) et (D2)
Ca donne :

soit |15+c| = 25 , soit c = 10 OU c = -40
On a dc : (D1) 4x+3y+10=0 et (D2) 4x+3y-40=0
Q2a : Soit M (x;y) un point de (d) et  :
: un vecteur directeur de (D). Comme (d)
 (D), on a
(D), on a , soit :
[(x-3) +(y-1)
+(y-1) ].(-3
].(-3 +4
+4 )=0
)=0
ce qui revient à écrire, puisque le plan est muni d'un r.o.n. :
-3(x-3)+4(y-1) =0  -3x+4y+5 = 0
-3x+4y+5 = 0
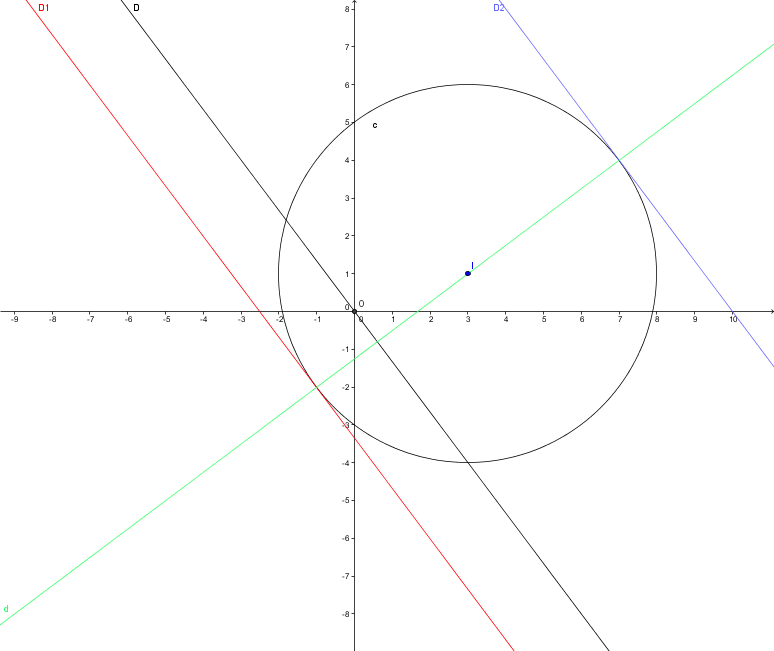
Q2b)
Ah Sirène et ses pbs de maths infaisables..
les coordonnées x et y de a et de B sont celles qui vérifient simultanément
Je pense qu'en 1S on sait pas résoudre un tel système, moi même il faudrait que je fasse une recherche ds mes livres ou sur internet, et je pense que c'est pr ça que la réponse est donnée tt de suite après, ce qui "colle" avec le graphique.
Bon je termine
Q2c
(D1) est la droite qui pase par B (-1;-2) ; son équation cartésienne est dc de la forme
4x+3y+m=0 . Pr déterminer m, on remplace x et y par les coordonnées d'dun point connu qui appartient à (D1), en l'occurrence B. on a dc : -4-6+m = 0, soit m = 10 et
(D1) : 4x+3y+10 = 0, ce qui confirme le résultat que j'avais trouvé en Q1c alors que je viens de comprendre que en Q1c, il s'agit "juste" de tracer (D1) et (D2) géométriquement et non analytiquement comme je l'avais fait.
(D2) est la droite qui pase par A (7;4) ; son équation cartésienne est dc de la forme
4x+3y+n=0 . Pr déterminer n, on remplace x et y par les coordonnées d'dun point connu qui appartient à (D2), en l'occurrence A. on a dc : 28+12+n = 0, soit n = -40 et
(D2) : 4x+3y-40= 0, ce qui confirme le résultat que j'avais trouvé en Q1c
Q3a
Cf mes explications générales sur les calculs de distance ds un plan muni d'un r.o.n.
, avec ici x=7 et y = 4
, avec ici x=-1 et y = -2
Q3b
La distance d'une première droite à une autre droite est égale à la distance d'un point de cette première droite à l'autre droite. on a dc déjà les réponses cherchées.
Si ton/ta prof vs dit comment résoudre le système de mon message de 18 h 53, je suis TRES preneur de la solution 
Salut 
On procède par substitution pour résoudre le systême de 18h53 , tu auras un trinôme du second degré.
Et tu en déduis l'autre valeur ensuite 
OK bah c'est tt à fait accessible à une élève de 1S
Tu peux poser par ex et tu vas aboutir après réduc au même dénominateur à l'équation x²-6x-7 = 0 ; tu sais sûrement la résoudre, on retrouve facilement nos 2 abscisses et p.c. les ordonnées correspondantes en reprenant la 2ème équation originale du système (mais tu peux prendre la 1ère si tu veux

 )
)
Merci encore à Olive  et
et  à moi de ^m' être laissé impressionné par x² et y² ensembles (j'ai repensé à des coniques....à tort)
à moi de ^m' être laissé impressionné par x² et y² ensembles (j'ai repensé à des coniques....à tort)
BOn bah super comme ça 
j'ai fait la substitution direct de y par x à partir de l'équation 2 ds la 1 ; on trouve pareil au final
Globalement ça va plutot bien, je te remercie ! Et toi, tu t'accroches ; ça se presente bien ce 2ème semestre ?
(et les khôlles, tu survis ...)


Bonsoir pppa !
Je viens de lire vos éléments de réponses à propos de cet exercice.
Il n'y a rien à redire ! Après avoir fait moi-même les calculs, nous trouvons exactement les mêmes réponses.
De plus, tout est bien rédigé, expliqué... Du super boulot pppa  .
.
En revanche, il y a juste un petit détail qui m'embête concernant la question 2)b) sur ce fameux système.
Je comprends tout à fait la logique de faire un système dans ce cas de figure, je l'approuve d'ailleurs, par contre, même avec vos indications et celles d'olive_68, je n'arrive vraiment pas à le résoudre après développements et factorisations...
Je n'arrive pas à obtenir le résultat voulu.
Pourriez-vous m'aider sur ce point pppa ?
Cordialement 
Egalement, en plus de m'expliquer le système de la question 2)b).
Pourriez-vous me dire comment vous avez trouvé : avec cette formule ?
ssi
ssi
ssi
Bonsoir Sirène
pr ta 1ère question, est-ce QUE tu es d'accord que ce qui découle de la 2ème équation du système qui reprend les consitions à satisfaire par x et y pr être simultanément sur (AB) et sur le cercle (C) ?
Ta 2ème question me surprend ! c'est du niveau collège ça !
|15+c| = 25 (1)
soit 15+c  0 et (1) s'écrit 15+c= 25 soit c = 10
0 et (1) s'écrit 15+c= 25 soit c = 10
soit 15+c < 0 et (1) s'écrit -15-c= 25 soit c = -15-25 = -40
Non ?
D'accord pour la réponse à ma deuxième question  .
.
J'avais zappé la nuance avec les valeurs absolues, effectivement...
Concernant le système, oui je suis d'accord avec vous pour l'écriture de y mais lorsqu'il s'agit de développer puis réduire au même dénominateur avec cette expression là de y, je n'y arrive. Je suis bloqué sur une fraction exorbitante.. Je n'arrive pas à simplifier.
Un petit découpage de ce système de votre part serait sympathique pour pouvoir mieux comprendre la manière dont vous procédez pour arriver au résultat à obtenir (?)  .
.
lorsqu'il s'agit de développer puis réduire au même dénominateur avec cette expression là de y, je n'y arrive
Le dénominateur commun à utiliser, c'est 16 (4²)
pardon si je me trompe mais je suis persuadé que t'a pris 4 ....
après c'est que du calcul algébrique et tu dois aboutir à 25x²-150x-175 = 0
ce qui peut encore se simplifier en divisant (les 2 membres, mais en fait ici que le premier) par 25, et tu résouds une équation bien à ta portée :
x²-6x-7 =0 qui admet 2 racines réelles, soit les 2 abscisses des points cherchés ; on en déduit alors facilement leurs ordonnées resp.
A toi

Ok cool  Tu fais quoi exactement cette année ?
Tu fais quoi exactement cette année ?
Ca va mieux quand même qu'au début de l'année  Merci ^^ (Ca dépend des khôlles, celles de maths j'aime bien, le reste je pourrais m'en passer
Merci ^^ (Ca dépend des khôlles, celles de maths j'aime bien, le reste je pourrais m'en passer  .. )
.. )
>>Olive :Tiens je pensais t'avoir répondu vers 17 h 30 ; apparemment mon message a été mal validé... pas grave.
Oui alors je disais que je suis pr ma part déjà ds la vie active.
Content que tu t'accroches. Tu as une idée de la spé que tu vas faire ou que tu voudrais faire ou qu'on va te laisser faire ?
Et si c'est pas indiscret , t'es ds quel lycée ? (68 c'est ton dept ?)
>> Sirène
excuse-ns de ces échanges loin de ton pb, mais avec Olive on se connait de puis qq tps (mes débuts sur le forum en fait) et on a pas mal sympathisé ; entre gens qu'aiment bien les maths...

 )
)
Bonsoir pppa !
Voilà j'ai réussi à me débrouiller et à retomber sur mes pattes pour le système.
Maintenant nous pouvons considérer que l'exercice et par conséquent le topic est terminé !!
Je vous remercie infiniement pour l'aide que vous m'avez apporté pppa et olive_68, j'en suis très reconnaissant...
En attendant, j'ai encore et encore un autre exercice pour vous pppa 
Vous allez peut-etre vous dire "Punaise, il y en a marre de Sirene  " mais comme vous rédigez bien et que vos réponses sont également bonnes, autant gardez les bonnes habitudes
" mais comme vous rédigez bien et que vos réponses sont également bonnes, autant gardez les bonnes habitudes  .
.
L'exercice que je vous propose, par contre, est un peu plus complexe mais plus court que celui-ci, il englobe produit scalaire et angles orientés (trigo).
Le voilà sur ce lien : ![]() Problème de 1e S : Produit scalaire et Angles orientés
Problème de 1e S : Produit scalaire et Angles orientés
En vous attendant vous et peut-etre olive_68 sur ce lien,
Passez une bonne soirée 
Cordialement