Inscription / Connexion Nouveau Sujet
Problème de 1e S : L'Hyperbole
Bonjour à tous,
J'ai actuellement un DNS de mathématiques à réaliser.
L'un des exercices sur lequel porte ce DNS propose un problème d'Hyperbole, alliant limites ; fonctions ; dérivations.
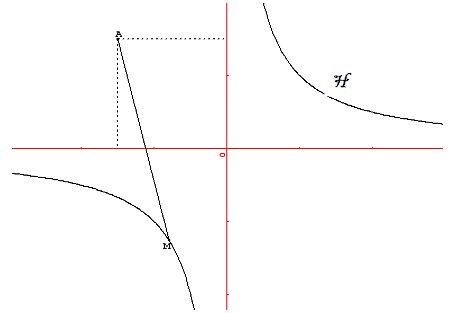
En voici l'énoncé (figure jointe ci-dessous) :
Prérequis :
Dans un repère orthonormal du plan, deux droites, non parallèles à l'axe des ordonnées sont perpendiculaires si et seulement si le produit des coefficients directeurs de ces deux droites est égal à -1.
Exercice :
Dans un repère orthonormal (O; ;
; ), on considère l'hyperbole H d'équation y =
), on considère l'hyperbole H d'équation y = et le point A
. A tout réel x non nul, on associe le réel f(x) tel que f(x) = AM2, où M désigne le point d'abscisse x de l'hyperbole H.
1. Exprimer f(x) en fonction de x.
2. Déterminer les limites de f aux bornes des intervalles de définition.
3. Calculer f '(x).
4. a. Factoriser f '(x).
b. En déduire le signe de f '(x) et les variations de f.
c. Etablir le tableau complet des variations de f.
5. Tracer Cf dans un repère dont l'échelle choisie est "astucieuse".
6. Soit g(x) =
a. Déterminer les variations de g.
b. Construire le tableau de variations de g.
7. En déduire qu'il existe deux points M1 et M2 de l'hyperbole H, d'abscisses respectives x1 et x2, où la distance AM est minimale.
8. a. Montrer que la tangente à H en M1 est orthogonale à la droite (AM1).
b. Montrer que la tangente à H en M2 est orthogonale à la droite (AM2).
Bonsoir Sirène
je vais ESSAYER de t'aider sur ce pb riche en notions d'analyse pr le programme de 1S.
Q1 : la réponse de Yzz est bonne, on pouvait s'en douter vu son niveau d'études, reste qd même à préciser, pr être complet et montrer que tu suis bien
- que ce calcul de (carré de) distance de AM n'est possible de cette façon que parce que le plan ds lequel on travaille est rapporté à un r.o.n.
- et que il faut qd même développer le résultat et simplifier au max pr une réponse qui à mon avis facilitera les calculs de limites
Dc j'écrirais : , f s'exprimant ainsi ss forme de FRACTION RATIONNELLE
Q2 Le dddf de f est  *, les bornes du dddf à considérer sont dc :
*, les bornes du dddf à considérer sont dc :
- ; +
; + ; 0- ; 0+
; 0- ; 0+
Pr les 2 premiers calculs de limite, il faut utilser le tm selon lequel en l'infini, la limite d'une fonction rationnelle est la même que celle du rapport de ses termes de + haut degré au numérateur et au dénominateur
Dc
De même :
Les limites de f(x) en 0, que ce soit par valeurs supérieures ou inférieures, reviennent à considérer le rapport , et on sait que les limites en 0 de cette fonction de référence qu'est la fonction inverse du carré sont +

Dc les 4 limites cherchées sont égales à + .
.
Voilà, pr l'instant je m'interromps mais j'esasierai de continuer ce soir.
C'est pr qd ton DNS ?
Q3 : pr déterminer f'(x), on peut partir de la forme donnée par Yzz, ça peut paraître + simple mais faut être très habile ds le maniement du "calcul" de dérivées, ou de f ss forme de fraction rationnelle, moi je préfère, c'est un peu + long mais - périlleux.
On pose u(x) = 2x4+6x3+9x²-6x+2 v(x) = 2x², et on applique la formule de déivation d'une fonction fraction rationnelle f' = (u'v-uv')/v²
Sauf erreur,(mais je suis quasi sûr que c'est bon) après développements et simplifications, tu dois trouver
Q4a : je commence à avoir des doutes sur ce que je fais , si ça correspond à ce qui est attendu. J'ai réussi à factoriser f'(x), mais qd j'étais en 1ère je sais pas si j'aurais su le faire, et si je m'en suis sorti assez rapidement c'est en utilisant une technique que jj'apprenais en 1ère, très pratique,et qui aujourd'hui n'est plus utilisée que ds le supérieur : la division de polynômes.
On peut tjs essayer par identification, mais c'est bcp + long et "vachement" - évident, parceque on part d'un pnm de degré 4 au numérateur (et avec la forme ed Yzz, c'est pas + évident je trouve).
Alors, comment factoriser ce numérateur de degré 4 avec un terme de degré 3 ??
J'ai vu(assez vite) que -2 est une racine censée être évidente. (x+2) est dc un facteur et on se retrouve avec f'(x)=(x+2)(2x3-x²+2x-1)/x3
T'as appris je pense le tm selon lequel ds  , tt pnm peut se décomposer en facteurs de degrés max 2., dc ce facteur de degré 3 peut encore se factoriser.
, tt pnm peut se décomposer en facteurs de degrés max 2., dc ce facteur de degré 3 peut encore se factoriser.
J'ai vu (un peu moins vite) que 1/2 est une racine de ce pnm de degré 3
et le facteur restant est 2x²+2 = 2(x²+1)
On a dc
Je suis quasi sûr de ma réponse, mais franchement je me demande si on peut attendre ça d'un(e) élève de 1S en 2010, sauf à faire faire de longues recherches et de lours calculs !

On continue ? parce que je me demande si je suis pas passé à côté de qqc de + simple


Bonsoir pppa,
Tout d'abord mille et un mercis pour votre aide..
J'ai regardé ce que vous avez écrit à propos des 3 premières questions.
Il y a deux choses qui me "tracassent" :
* Etes-vous sûr que
lorsque x < 0 ?
* Etes-vous sûr de votre calcul de f '(x) ?
J'ai fait moi aussi le calcul de f '(x) sur une feuille mais j'obtient un résultat peu satisfaisant.
En réalité je bloque sur la dérivée de 2x4, quelle est-elle ? Est-ce 8x2 ?
A partir de ce point, je saurai réaliser ce calcul à mon avis.
Bonsoir Sirène
ça peut paraitre présomptueux mais je suis quasi sûr de mes réponses, moins sur la manière optimale de les trouver, et je pense que c'est un exercice pas particulièrement difficile mais lourd en calculs et recherches, surtt avec le programme actuel de 1S.
Mais encore une fois j'ai pu passer à côté de qqc de plus simple, et si c'est le cas je m'en excuse par avance.
+ précisément :
1/ pr le calcul de la limite : un carré étant tjs positif qqs le signe de la variable.....tu vois ce que je veux dire.
2/ pr la détermination de f' ; je me permets de dire que je suis sûr car je l'ai vérifié avec un logiciel traceur de graphe qui trace aussi les fonctions dérivées des fonctions, et ça colle...
Dc veux-tu qu'on continue à partir de la 4b, si t'es d'accord avec ts les résultats d'avant ?

En réalité je bloque sur la dérivée de 2x4, quelle est-elle ? Est-ce 8x2 ?
Donc (2x[sup]4)'=2
 4x3=8x3.
4x3=8x3.Ah oui j'avais oublié de répondre à ça ! Excuses.
Yzz, qu'est-ce tu penses de mes développements jusqu'à présent, notamment de méthode pr factoriser f'. Si c'est juste, je suis pas sûr qu'en 1S on sache faire aujourd'hui comme j'ai fait
merci
bonne journée.
D'accord pppa,
Je vous fais confiance, jusque là je n'ai pas eu de problème avec vos raisonnements.
Nous pouvons donc continuer à partir de la 4b), je suis d'accord avec vos résultats, d'autant plus qu'ils ont été vérifiés par un logiciel  .
.
Continuons  .
.
Bonsoir Sirène
allez, on y retourne.
Q4b
signe de f'(x) : .
Pr moi, il faut scinder l'étude du signe en 2 parties, selon que x
 -* ou x
-* ou x
 +*, ce qui permet de "fixer" le signe du dénominateur x3, qui est resp. - et +.
+*, ce qui permet de "fixer" le signe du dénominateur x3, qui est resp. - et +.
Au numérateur les facteurs 2 et x²+1 sont tjs >0.
Le signe de f'(x) se détermine dc en se restreignant à l'étude du signe de , puis de prendre les résultats tels que trouvés sur
 +*, et de changer de signe sur
+*, et de changer de signe sur  -*
-*
D'accord ? Ca c'est assez facile.
Oui je suis d'accord avec ce que vous avez dit pppa.
Désolé de ce retard, je passais mes TPE et je voulais me consacrer un petit peu à cela  .
.
Maintenant que l'examen est passé, nous pouvons donc continuer ce fameux DNS  .
.
A bientôt pour le reste des questions !
Cordialement.
Oui ca s'est bien passé.
Le thème que le groupe a choisi était le tsunami.
Nous avons bien géré.
Allez on peut repartir tranquilement vers les questions suivantes maintenant  .
.
Cordialement pppa
Bonjour sirene
on va essayer de le terminer.
est-ce que tu as fait le tb de variations de la 4c qui découle du résultat de la 4b ?
Oui Oui ne vous inquietez pas.
A partir du moment où la réponse à la 4b) est bonne, la réponse à la 4c) est un jeu d'enfant puisque, en effet, elle en découle.
Nous pouvons passer à la suite.
bonjour
j'ai travaillé sur les Q5 et 6 ; les résultats du graphiquent ne colent pas avec ce que j'ai trouvé avant ==> je suis embarassé et c'est pr ça que je tardais à te répondre
Je suis vraiment désolé Sirène, il y avait lgtps que ça m'était pas arrivé mais là je suis un peu perdu ; je ne retrouve plus la cohèrence de mes résultats avec les graphiques que j'ai faits !  malgré vérifications.
malgré vérifications.
Prtant j'aime pas capituler, surtt en maths. Dis moi c'est pr qd ce DNS ? Si j'ai le tps je rechercherai encore, mais....

ca me fait peine pr toi qui attendait de l'aide efficace.. 
a bientôt p.e.
excuses encore
ciao !
Salut,
--->pppa:
Je ne t'avais pas répondu, car je n'avais pas pris le temps de lire ton travail; et je te prie de m'en excuser...
J'imprime tout le bazar, et je regarde ça dans la journée, retour en fin d'après-midi, promis!!! 
...Vite fait, avant de partir au boulot:
Bravo pppa sur tout ce que tu as fait, et notament sur la factorisation de f'(x): pas sûr que j'y soie arrivé aussi facilement que toi!
4b et 4c: faire un tableau de signes avec (2x-1); (x+2) et x3; on trouve f'(x) négative sur ]-oo;-2] et ]0;1/2] positive sur le reste (sans oublier la valeur interdite...) D'où les variations de f; et les deux minimums (en -2 et 1/2) pour lesquels f vaut 17/4.
6: formule ( u)'=u'/(2
u)'=u'/(2 u): ainsi, g'(x) a le même signe que f'(x); tab. var. semblable à adapter...
u): ainsi, g'(x) a le même signe que f'(x); tab. var. semblable à adapter...
Faut que j'y aille!!! 
>>Yzz :
Merci bcp d'intervenir et je t'en prie tu n'as pas à t'excuser
on trouve f'(x) négative sur ]-oo;-2] et ]0;1/2] positive sur le reste (sans oublier la valeur interdite...) D'où les variations de f;
Voilà où j'en suis rendu ; le pb, c'est que qd j'arrive à la Q5 - tracé de Cf je ne retrouve pas ces variations. Je l'ai fait abvec le logiciel SQN de patrice rabiller
J'aboutis à une parabole très haute - genre x4 - le 0 doit être exclu mais on voit pas assez bien, dc aucune inversion de croissance sur les intervalles précités (ou alors je passe à côté de qqc...). Et alors j'ai voulu envoyer les graphiques à Sirène en format .png, mais il faut réduire les dimensions et les tracés deviennent degueulasses, même qd je reviens au format initial.
tt ça explique que je suis plutot désappointé sur ce sujet, prtant j'aimearais bien qu'on le termine, à ns 3 on va bien y arriver

la factorisation de f'(x): pas sûr que j'y soie arrivé aussi facilement que toi!
A suivre dc ; merci de ns donner un peu de ton tps

(juste histoire de remonter le topic, si besoin...)
pour la factorisation de f'(x): il ne me semble pas que l'on puisse demander cela en 1èreS, sans indication préalable.
En fait, tout dépend de ce qui a été fait en classe sur le sujet, et notamment l'emploi de logiciels ou de clculatrices performantes (La TI NSpire par exemple, qui donne la facto sur demande).
il ne me semble pas que l'on puisse demander cela en 1èreS, sans indication préalable
clculatrices performantes (La TI NSpire par exemple, qui donne la facto sur demande).
Ah ouais ! Je ne connaisais pas cette calculatrice ; elle est nouvelle ? Et tu crois que ts les élèves en sont équipés, ou peuvent se la payer (puisque les régions pleurent qu'elles ont plus de sous, et qu'elles vont en avoir encore moins..)
A + tard
(manip hasardeuse, je reprends
J'ai fait la courbe, mais je n'arrive pas à la faire suivre (trop lourde); elle correspond à mon tab var sans problème...
As-tu bien mis des parenthèses partout, notamment au dénominateur?
As-tu bien mis des parenthèses partout, notamment au dénominateur?
Bah non, j'en ais pas mis, puisque c'est le monôme 2x²...



Tu crois que ça viendrait de là

je réessaye avec les parenthèses et on en reparle
A tt à l'heure
 OK Compris ; je retrouve bien les variations attendues d'après f'(x)
OK Compris ; je retrouve bien les variations attendues d'après f'(x)
en mettant le parenthèses au dénominateur.
Vaï  ! mais intuitivement j'aurais pensé que là c'était pas la peine de les mettre au dénominateur..
! mais intuitivement j'aurais pensé que là c'était pas la peine de les mettre au dénominateur..
Merci pr ton précieux conseil Yzz..

Bonjour à vous Yzz et pppa,
Concernant la calculatrice, je ne possède qu'une Graph 35+, conseillée et par mon professeur de Maths et par l'établissement.
Sinon pour répondre à pppa, mon DNS est pour après les vacances scolaires, cependant je pars en vacances dès dimanche jusqu'à vendredi d'après. Je n'aurai donc pas de connexion internet dans cet intervalle.
En outre, concernant le DNS, il est vrai que nous n'avons pas vu la division polynomiale. En revanche, mon professeur de Maths considère ses DNS comme des exercices de recherches où des exercices "plus poussés", d'où les problèmes avec un degré de difficulté assez conséquent que j'avais posté il y a quelques semaines. Ainsi, je pense qu'une division polynomiale pourrait être faisable dans ces circonstances.
Après, il faut juste que les calculs soient bons 
Comment pouvez-vous savoir qu'il y a un problème à la question 5 si, pour vous, tous les calculs précédents sont bons ?
Si vous bloquez sur une question, vous pouvez en passer outre, d'autant plus que les questions suivantes sont indépendantes des précédentes  . Ce n'est pas bien grave. Quitte à revenir dessus une fois que tout est bouclé
. Ce n'est pas bien grave. Quitte à revenir dessus une fois que tout est bouclé 
Cordialement
Bon, garde ta chemise  , mais cette syntaxe, c'est spécifique à SQN , ou....? attends, j'ai un autre logiciel, je vais tester
, mais cette syntaxe, c'est spécifique à SQN , ou....? attends, j'ai un autre logiciel, je vais tester
Bonjour Sirène
Comment pouvez-vous savoir qu'il y a un problème à la question 5 si, pour vous, tous les calculs précédents sont bons ?
non je me suis trompé ds la syntaxe du logiciel ; excuses
>>Yzz : eh oui c'est pareil avec l'autre logiciel ; Eh beh.. je suis aps près de l'oublier ça !
merci
Bon bah on va pouvoir reprendre..
--->pppa: C'est vvalable partourt, c'est juste un pb de priorités opératoires, les logiciels font les opérations dans l'ordre, et de gauche à droite s'il n'y a pas de parenthèses: 3/2 5=1,5
5=1,5 5=...
5=...
--->sirene: pas de pb pour la 5, si ce n'est que je suis infoutu de faire suivre le graphique... Mais ça colle bien avec l'étude précédente. Tu as le tableau de variation correct?
La suite:
Comme g(x) =  f(x), on a: g'(x) = f'(x)/2
f(x), on a: g'(x) = f'(x)/2 f(x).
f(x).
Et donc g'(x) a le même signe que f'(x).
Ainsi, g a les mêmes variations que f, et aussi les mêmes limites. Il faut juste re-calculer les valeurs des minimums: g(-2)=g(1/2)=( 17)/2.
17)/2.
Regarde la dérivée de g dans mon message précédent: son numérateur est f'(x) et son dénominateur est positif (c'est 2 fois la racine de f(x), qui est positive). Donc son signe est celui de f'(x).
pour ses limites, un exemple:
vers + ,
,
limite de f = + et g =
et g =  f, donc limite de g = +
f, donc limite de g = + .
.
Voilà ce qu'il reste après avoir pas mal rogné pr être aux dimensions image ile: la courbe en noir c'est l'hyperbole H. Le principal y est je pense.
Ciao !
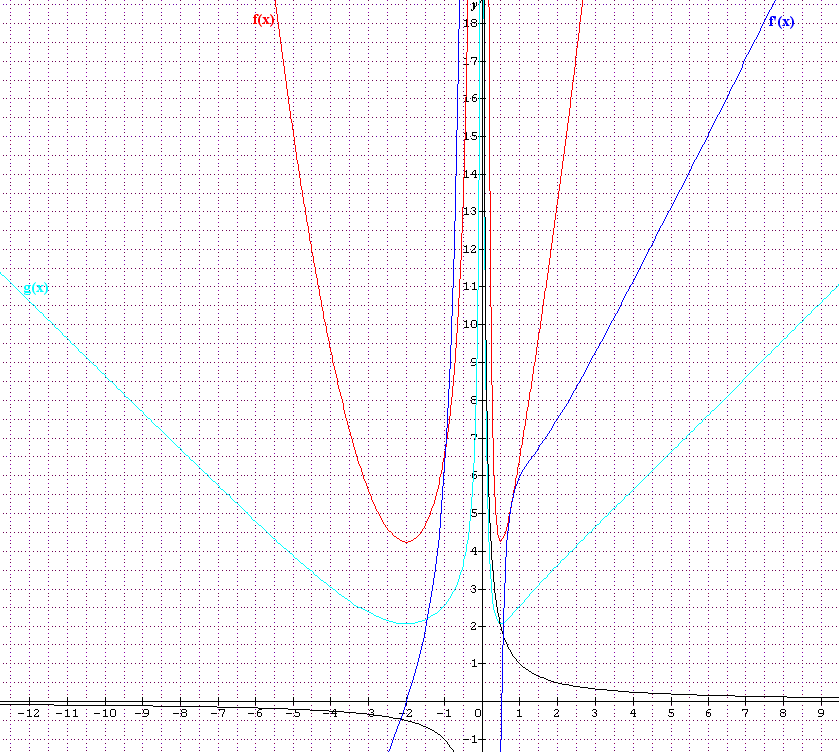
Pas mal du tout cette courbe pppa :p
Maintenant que le traçage de Cf a été effectué nous pouvons passer aux questions suivantes 
Bonjour
Sirene
Q6 : je reprends ce qu'a dit Yzz
dc g' est du même signe que f'
dc g a les mêmes variations que f
Q7 On a vu que f passe par 2 minima : (-2;17/4) et (-1/2;17/4)
Or f(x)=AM², dc
Puisque g a les mêmes variations que f, , g admet aussi 2 minima qui ont même abscisses que ceux de f, soient les points de coordonnées :
(-2; 17/2) et (-1/2;
17/2) et (-1/2; 17/2).
17/2).
Les 2 points cherchés sont resp. M1et M2, i.e. les 2 points de H dt les coordonnées sont resp :
Ce sont ces 2 points de H pr lesquels la distance AM, ie de A à la c.r de H, est minimale.
Tu peux le vérifier sur le graphique d'avant hier même si j'ai pas placé le point A.
Q7 On a vu que f passe par 2 minima : (-2;17/4) et (-1/2;17/4)
Pr le 2ème point c'est 1/2 d'abscisse et non pas -1/2, excuses
On a vu que f passe par 2 minima : (-2;17/4) et (1/2;17/4)
Puisque g a les mêmes variations que f, g admet aussi 2 minima qui ont même abscisses que ceux de f, soient les points de coordonnées :
(-2;17/2) et (1/2;17/2)
Qu'entends-tu par "2 minima" ?
Que veulent dire tes abréviations : "i.e." et "c.h." ?
Merci beaucoup pppa
Bonjour Sirene
Un minimum , des minima (Cf tes cours ou tes souvenirs de latin) c'est un point de la Courbe Représentative (c.r.) d'une fonction pr lequel l'ordonnée, dc la valeur prise par la fonction , est minimale
i.e est une abbréviation (qui vient aussi du latin, assez couramment utilisée pr les gens de ma génération en tt cas) qui signifie littéralement Id Est, ce qui se traduit par "c'est à dire" (prtant j'étais pas un "grand" latiniste)
Il ne restera plus qu'à résoudre la question des tangentes, j'essaye de faire ça cet AM, à moins que Yzz n'intervienne entre tps.
Sinon ça va, tu suis ?
Q8a
Cherchons une équation de la droite (AM1) : elle est dirigée par , dc le vecteur
 de coordonnées
de coordonnées est aussi un vecteur directeur de(AM1), ce qui permet de savoir que l'équation cherchée est de la forme y=4x+b. pr trouver B, on sait que A appartenant à la (AM1),, l'équation vérifie :
, soit b = 15/2 (quoique cette recherche de b n'est pas nécessaire pr répondre à la question comme on va le voir + tard, mais bon, moi je l'ai fait pr me vérifier sur mon logiciel, et dc c'est bon).
L'équation de la tangente à (H) en M1(-2;-1/2) est de la forme (Cf ton cours que tu connais j'en suis sûr, du moins j'espère) :
y = h'(M1).(x-xM1) + h(M1), ce qui donne:
, soit
Le plan ds lequel on travaille étant rapporté à unrepère orthonormé, 2 droites de ce plan sont  ssi le produit de leurs coeff directeurs resp. est égal à - 1
ssi le produit de leurs coeff directeurs resp. est égal à - 1
Le coeff. dir de (AM1) c'est 4
Le coeff. dir de la tg à (H) au pt d'abscisse -2, c'est -1/4.
Le produit de ces 2 coeff dir vaut bien -1 ; CQFD
D'accord ?
Tu fais pareil pr M2, et l'exercice est TERMINE.
Bien sûr, si tu as des questions et que je peux y répondre, n'hésite pas
Et bravo pr ta persévérence pr un exercice difficile en 1ère
Bonjour pppa !
J'ai réussi à avoir une connexion internet pendant 2h aujourd'hui.
Je serai de nouveau sur ilemaths en fin de semaine.
Je viens de lire ce que vous m'avez posté concernant la question 8a) mais je n'ai pas très bien compris votre raisonnement..
Si vous pouviez me le refaire avec (AM2) ca serait sympa de votre part  .
.
Cordialement,
Sirene 



