Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première Produit scalaireTopics traitant de Produit scalaire [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

Problème de 1e S : Produit scalaire et Angles orientés

Posté par
Sirene 29-04-10 à 23:13

Bonjour à tous,

J'ai actuellement un DNS de Mathématiques à réaliser.
L'un des exercices de ce DNS porte sur un problème alliant produit scalaire et angles orientés.

En voici l'énoncé :

Les deux parties de cet exercice sont indépendantes.

Partie A

1.     a. Démontrer que si et sont deux vecteurs, alors : (+)•(-) = ||||2 - ||||2.

        b. En déduire que ||||2 = ||||2 si, et seulement si, (+) et (-) sont orthogonaux.

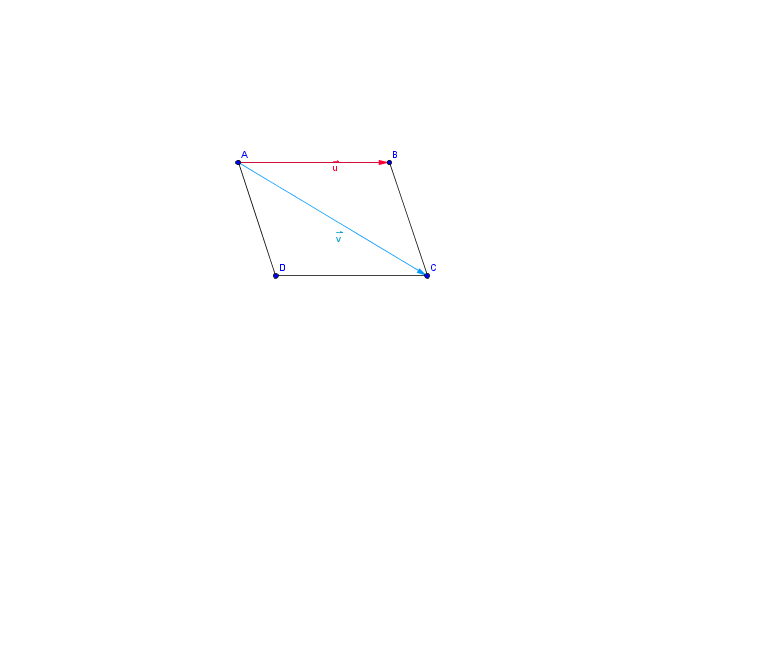
2. Application : Soit un parallèlogramme ABCD. On pose : = \vec{AB}   et   = \vec{AC}

        a. Construire + et -.
      
        b. Montrer que \vec{AD}  et  \vec{BC} sont orthogonaux si, et seulement si, AB = AC.

Partie B

1. Vérifier que \frac{5\pi}{12} = \frac{\pi}{4} + \frac{\pi}{6}

2. En déduire la valeur exacte de \cos(\frac{5\pi}{12}) et de \sin(\frac{5\pi}{12})

Posté par
pppare : Problème de 1e S : Produit scalaire et Angles orientés 29-04-10 à 23:46

bonsoir  

partie B
1/ calcul niveau collège ; réduire au même dénominateur
2/
2$\cos(\frac{5\pi}{12})=\cos(\frac{\pi}{4}+\frac{\pi}{6})=(\cos\frac{\pi}{4}\times \cos\frac{\pi}{6})-(\sin\frac{\pi}{4}\times \sin\frac{\pi}{6})=(\frac{\sqrt{2}}{2}\times \frac{\sqrt{3}}{2})-(\frac{\sqrt{2}}{2}\times \frac{1}{2})

==> \red\fbox{2$\cos(\frac{5\pi}{12})=\frac{\sqrt{6}-\sqrt{2}}{4}

2$\sin(\frac{5\pi}{12})=\sin(\frac{\pi}{4}+\frac{\pi}{6})=(\sin\frac{\pi}{4}\times \cos\frac{\pi}{6})+(\cos\frac{\pi}{4}\times \sin\frac{\pi}{6})=(\frac{\sqrt{2}}{2}\times \frac{\sqrt{3}}{2})+(\frac{\sqrt{2}}{2}\times\frac{1}{2})

==> \red\fbox{2$\sin(\frac{5\pi}{12})=\frac{\sqrt{6}+\sqrt{2}}{4}

Pr la partie A je verrai demain

Buona notte  ; ciao !

Posté par
Sirenere : Problème de 1e S : Produit scalaire et Angles orientés 01-05-10 à 16:33

Bonjour pppa !

Concernant la partie B de l'exercice ci-dessus, je suis entièrement d'accord avec vos éléments de réponses. Nous pouvons passer maintenant à la partie A .

Cordialement

Posté par
pppare : Problème de 1e S : Produit scalaire et Angles orientés 01-05-10 à 17:18

Bonjour Sirène

comme promis, je reprends la partie A

Q1a : il suffit d'appliquer l'identité remarquable (a+b).(a-b) = a²-b² qui s'applique au calcul vectoriel. On aboutit alors à ²-², sachant que le carré scalaire d'un vecteur est le nombre réel égal au carré de sa norme, d'où l'égalité à démontrer

Q1b : ||||² = ||||²
||||²-||||² = 0
(+).(-)=0 (Cf Q1a)
Or le p.s. de 2 vecteurs (ici les vecteurs (+) et (-)) est nul ssi ces vecteurs sont orthogonaux.
Cqfd !

OK ?

Posté par
pppare : Problème de 1e S : Produit scalaire et Angles orientés 01-05-10 à 17:26

Q2

t'es sûr de ton énoncé ? On peut tjs construire les 2 vecteurs demandés, mais les conditions demandés en Q2b me paraissent incompatibles avec le fait que ABCD soit un parallélogramme, non ?

Posté par
pppare : Problème de 1e S : Produit scalaire et Angles orientés 01-05-10 à 17:50

tu vois ce que je veux dire ?

Problème de 1e S : Produit scalaire et Angles orientés

Posté par
Sirenere : Problème de 1e S : Produit scalaire et Angles orientés 02-05-10 à 23:43

Bonsoir pppa !

Après comparaison ilemaths-énoncé, j'en déduis que j'ai recopié l'énoncé scrupuleusement. Il n'y a pas fautes de frappe ni d'erreurs de ma part pour les questions 2a) et 2b).

En revanche, je revendique une erreur de ma part, cette fois-ci concernant la question 1b) :

Citation :
1b. En déduire que ||||2 = ||||2 si, et seulement si, (+) et (-) sont orthogonaux.


Il ne s'agit pas de ||||2 = ||||2 mais de |||| = ||||.

Voilà :S.

Cordialement

Posté par
pppare : Problème de 1e S : Produit scalaire et Angles orientés 02-05-10 à 23:54

Bonsoir sirene

Excuse-moi mais
1/ ds un prlgm ABCD, je vois pas comment on peut
  a/ avoir AB = AC  
  b/ avoir \vec{AD}\perp\vec{BC}
  d'où mon schéma

2/ E (E plan vectoriel associé au plan affine ds lequel est tracé le prlgm ABCD) on a ||||+ , dc
|||| = |||| ||||² = ||||², ce qui permet de poursuivre le raisonnement avec l'égalité établie précédemment

Posté par
Sirenere : Problème de 1e S : Produit scalaire et Angles orientés 03-05-10 à 21:44

Bonsoir pppa !

Petit récapitulatif :

1) a) = Terminé.
1) b) = Terminé.


2) a) et 2) b) = A mon avis, d'après la figure, vous ne comprenez pas que le vecteur AD et le vecteur BC puissent être orthogonaux, tout simplement parce que (d'après moi) vous avez mal placé les points du parallélogramme. Après avoir fait un petit schéma sur feuille, je me rends compte qu'en inversant les points C et D de votre figure, le problème pourrait être faisable et plus cohérent.

Qu'en dites-vous pppa ?
Si c'est cela, d'après moi, vous seriez capable de construire + et - + de démontrer que les vecteurs AD et BC sont orthogonaux ssi AB=AC.

Posté par
pppare : Problème de 1e S : Produit scalaire et Angles orientés 03-05-10 à 22:47

Bonsoir sirène

j'en dis que le prlgm ne s'appelle pas ABCD !

Posté par
Sirenere : Problème de 1e S : Produit scalaire et Angles orientés 03-05-10 à 23:14

Et moi j'en dis que je suis vraiment bête ...
J'ai vérifié au moins une dizaine de fois la concordance de l'énoncé avec celui que j'ai posté et je n'ai même pas été foutu d'avoir déceler une erreur que j'ai moi même faite !!!!!!!
En effet pppa, vous avez encore une fois de plus raison, il ne s'agit pas du parallélogramme ABCD mais du parallélogramme ABDC.

Donc rectification :

Citation :
2. Application : Soit un parallèlogramme ABCD. On pose :   = \vec{AB}  et   = \vec{AC}

        a. Construire + et -.
      
        b. Montrer que \vec{AD} et \vec{BC} sont orthogonaux si, et seulement si, AB = AC.



Il ne s'agit donc pas d'un parallélogramme ABCD mais d'un parallélogramme ABDC en effet.

Je suis vraiment désolé..
Je m'en veux car cela ne m'arrive pas trop souvent ce genre d'étourderies qui change complètement la donne.
Je vous prie de m'excuser pppa.
Maintenant que le problème est réglé, nous pouvons le terminer...

Cordialement

Posté par
pppare : Problème de 1e S : Produit scalaire et Angles orientés 03-05-10 à 23:26

OK mais je vais pas pouvoir le terminer ce soir ; mais promis je le ferai. Moi ça m'arrive pas souvent de laisser le travail inachevé , mais là ce soir je suis sur un pb ardu de nombres complexes ; si je le finalise ava,t minuit, c'est que je serais pas trop mauvais....

Est-ce que ça peut attendre demain le tien ?

Posté par
pppare : Problème de 1e S : Produit scalaire et Angles orientés 04-05-10 à 00:10

Waouh ! j'ai finalisé à 0h08 ; bon je vais pouvoir dormir tranquille, et je te dis non pas à demain mais à ds env. 18 heures, espérant que c'est pas trop tard  

Posté par
Sirenere : Problème de 1e S : Produit scalaire et Angles orientés 04-05-10 à 21:20

That's right ?

Posté par
pppare : Problème de 1e S : Produit scalaire et Angles orientés 04-05-10 à 22:54

Euh pas tt à fait, j'ai aps eu le tps ce soir qqs petits imprévus...

mais je lache pas l'affaire

Posté par
Sirenere : Problème de 1e S : Produit scalaire et Angles orientés 06-05-10 à 22:34

Bonsoir pppa !

Je ne voudrais ni vous brusquer, ni vous presser mais la date à laquelle je dois rendre ce DNS approche .
Surtout qu'il ne reste plus que 2 questions à résoudre...

En espérant que vous ne soyez pas mort

Cordialement

Posté par
pppare : Problème de 1e S : Produit scalaire et Angles orientés 06-05-10 à 22:47

C'est pr qd ton DNS (dis-moi pr lundi.. )

Hier j'ai fêté la victoire de Marseille au championnat de foot, ce ui rajouté à des imprévus m'a fait prendre du retard sur d'autres sujets dt le tien...

A bientôt  ..

Posté par
Sirenere : Problème de 1e S : Produit scalaire et Angles orientés 06-05-10 à 23:09

lundi.

Posté par
pppare : Problème de 1e S : Produit scalaire et Angles orientés 09-05-10 à 11:50

Bonjour Sirene

\vec{u}+\vec{v}=\vec{AD}

\vec{u}-\vec{v}=\vec{AD'}, D' symétrique de D par rapport à B

mais \vec{AD'}=\vec{AB}-\vec{AC}=\vec{CB},

Géométriquement, montrer que  \vec{AD} et \vec{BC} sont orthogonauxrevient à montrer que \vec{AD} et \vec{CB}, soit \vec{u}+\vec{v} et \vec{u}-\vec{v} sont orthogonaux.

Si ces 2 vecteurs sont orthgonaux, alors leur p.s. est nul ce qui revient à poser

(\vec{u}+\vec{v}).(\vec{u}-\vec{v})=0

²-²=0

² = ²

||||² = ||||²

|||| = |||| (Cf message du 02 mai)
soit AB = AC

Voilà, pas très difficile, faut juste avoir le tps.

Promesse tenue !

Posté par
Sirenere : Problème de 1e S : Produit scalaire et Angles orientés 09-05-10 à 19:32

Bonsoir !

Merci beaucoup d'avoir tenu votre promesse pppa.
C'est très gentil de votre part de répondre à chacun de mes exercices, d'y prendre du temps et de me répondre d'une manière parfaitement rédigée !
En attendant, j'ai encore et encore un autre exercice pour vous .
Celui-ci fait appel au chapitre sur les SUITES !

Voici le lien : Problème de 1e S : Suites

En espérant que vous me résolviez encore une fois cette exercice,
Je vous souhaite une bonne soirée !

Cordialement

Posté par
Sirenere : Problème de 1e S : Produit scalaire et Angles orientés 11-05-10 à 16:07

Ne m'oubliez pas, l'exercice est pour bientôt ...


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1760 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !