Inscription / Connexion Nouveau Sujet
Problème de maths appliqué a Excel
L'ensemble des programmes et fonctions seront écrits dans un module que vous nommerez "EXO1".
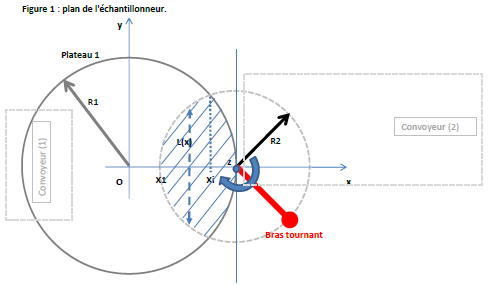
Sur une ligne de production, un échantillonneur est installé pour permettre une mise en emballage rapide et précise (cf. Figue 1). Il se compose d'un premier disque récepteur de pièces de rayon R1 = 1 m, alimenté par un convoyeur (1) à rouleaux. Ce disque récepteur est balayé à intervalle régulier par un bras tournant de longueur R2 permettant de ratisser le disque récepteur, les pièces interceptées tombant ainsi sur un autre convoyeur (2). L'axe (z) de ce bras sera positionné proche de la périphérie du disque récepteur.
Il sera commode de raisonner dans un repère orthonormé (O,[Ox),[Oy)) avec le centre du disque récepteur en (0, 0), l'axe du bras tournant en (R1, 0). On rappelle que l'équation d'un cercle dans un repère orthonormé est r²=x²+y², avec r le rayon du cercle. Par ailleurs, toute fonction f(x-x0, y) prend les mêmes valeurs que f(x ,y) avec une translation de x0.î sur l'axe [Ox), où î est le vecteur directeur unitaire de l'axe [Ox).
L'objectif de l'étude est de déterminer la longueur R2 du bras de telle manière que l'aire commune (aire hachurée sur la figure, on pourra la noter Ac) au disque récepteur et au disque de balayage du bras soit exactement la moitié de l'aire totale du disque récepteur (notée Ad), contrainte nécessaire pour une continuité du débit de pièces le long de la chaîne de production.
1- Quelle est l'expression de l'abscisse X1 en fonction de R1 et R2 ?
2- Quelle est la valeur de la surface du disque récepteur Ad ?
3- Une valeur de R2 comprise dans l'intervalle [0, 1] sera entrée en cellule A1 de votre feuille de calcul. Tracer sous Excel les Cercles de rayons R1 = 1 m et R2 = 1 m sur un même graphique « nuage de point », respectivement en bleu et rouge, en respectant le positionnement indiqué par la Figure 1, avec une précision de 0.1 m en abscisse. Vérifier que le traçage du cercle de rayon R2 est actualisé si la valeur de R2 est modifiée.
Le calcul de l'aire Ac nécessite l'intégration des abscisses X1 à R1 de la fonction L(x), L(x) étant la longueur du segment de corde obtenu par intersection du disque de balayage avec une droite verticale. Cette fonction L(x) prend deux formulations différentes L1(x) et L2(x) suivant que l'abscisse [X1, Xi] ou [Xi, R1].
4- Établissez la formulation de L1(x) en fonction de R2, x0 et x
5- Établissez la formulation de L2(x) en fonction de R1, et x
6- À partir de la condition d'intersection des deux cercles, déduire l'expression de Xi = Xi(R1, R2, x0)
7- Entrez la formule dans votre feuille pour calculer sa valeur en prenant R2 = 1 m.
8- Retrouvez ce résultat par utilisation du solveur, en spécifiant votre cellule cible, et votre cellule variable.
9- Écrivez une fonction personnalisée calcul_L1 permettant l'évaluation de la fonction L1(x)
10- Écrivez une fonction personnalisée calcul_L2 permettant l'évaluation de la fonction L2(x)
Bonjour quand même...
Tu devrais lire le mode d'emploi. La FAQ.
Tu y découvrirais qu'en plus de dire bonjour, il n'est pas inutile d'indiquer ce que tu as fait. Ce que tu as trouvé. Ce qui te bloque...
Et puis, il manque la figure.
Bonjour sanantonio312,
j'ai essayé de joindre une image mais ça ne fonctionnait pas, et je ne savais pas que le message etait posté :/
Je suis bloqué à la question 3) mais une petite confirmation des 2 premières serait bien aussi.
Et là normalement j'ai réussi a joindre la figure en pj.
1) Expression de l'abscisse X1 en fonction de R1 et R2 : X1 = R1 - R2
2) Surface du disque récepteur Ad : Ad = π R1² <=> Ad = π x 1² <=> Ad = π
Et complètement bloqué à la question 3) ... Je n'arrive pas du tout
Bonjour A tous
je vous joint un sujet que je doit corriger pour un élève à qui je donne des cours et je suis perdu
Merci d' avance à celui ou celle qui voudra bien m'aider
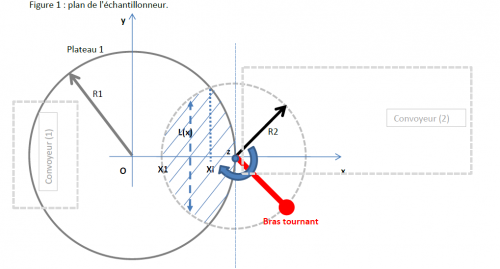
Sur une ligne de production, un échantillonneur est installé pour permettre une mise en emballage rapide et précise (cf. Figue 1). Il se compose d'un premier disque récepteur de pièces de rayon R1 = 1 m, alimenté par un convoyeur (1) à rouleaux. Ce disque récepteur est balayé à intervalle régulier par un bras tournant de longueur R2 permettant de ratisser le disque récepteur, les pièces interceptées tombant ainsi sur un autre convoyeur (2). L'axe (z) de ce bras sera positionné proche de la périphérie du disque récepteur.
Il sera commode de raisonner dans un repère orthonormé (O,[Ox),[Oy)) avec le centre du disque récepteur en (0, 0), l'axe du bras tournant en (R1, 0). On rappelle que l'équation d'un cercle dans un repère orthonormé est r²=x²+y², avec r le rayon du cercle. Par ailleurs, toute fonction f(x-x0, y) prend les mêmes valeurs que f(x ,y) avec une translation de x0.î sur l'axe [Ox), où î est le vecteur directeur unitaire de l'axe [Ox).
L'objectif de l'étude est de déterminer la longueur R2 du bras de telle manière que l'aire commune (aire hachurée sur la figure, on pourra la noter Ac) au disque récepteur et au disque de balayage du bras soit exactement la moitié de l'aire totale du disque récepteur (notée Ad), contrainte nécessaire pour une continuité du débit de pièces le long de la chaîne de production.
1- Quelle est l'expression de l'abscisse X1 en fonction de R1 et R2 ?
2- Quelle est la valeur de la surface du disque récepteur Ad ?
3- Une valeur de R2 comprise dans l'intervalle [0, 1] sera entrée en cellule A1 de votre feuille de calcul. Tracer sous Excel les Cercles de rayons R1 = 1 m et R2 = 1 m sur un même graphique « nuage de point », respectivement en bleu et rouge, en respectant le positionnement indiqué par la Figure 1, avec une précision de 0.1 m en abscisse. Vérifier que le traçage du cercle de rayon R2 est actualisé si la valeur de R2 est modifiée.
Le calcul de l'aire Ac nécessite l'intégration des abscisses X1 à R1 de la fonction L(x), L(x) étant la longueur du segment de corde obtenu par intersection du disque de balayage avec une droite verticale. Cette fonction L(x) prend deux formulations différentes L1(x) et L2(x) suivant que l'abscisse [X1, Xi] ou [Xi, R1].
4- Établissez la formulation de L1(x) en fonction de R2, x0 et x
5- Établissez la formulation de L2(x) en fonction de R1, et x
6- À partir de la condition d'intersection des deux cercles, déduire l'expression de Xi = Xi(R1, R2, x0)
7- Entrez la formule dans votre feuille pour calculer sa valeur en prenant R2 = 1 m.
8- Retrouvez ce résultat par utilisation du solveur, en spécifiant votre cellule cible, et votre cellule variable.
9- Écrivez une fonction personnalisée calcul_L1 permettant l'évaluation de la fonction L1(x)
10- Écrivez une fonction personnalisée calcul_L2 permettant l'évaluation de la fonction L2(x)
*** message déplacé ***
Ce sujet viens d'être traité: ![]() Problème de maths appliqué a Excel
Problème de maths appliqué a Excel
*** message déplacé ***
Il suffit désormais d'intégrer la fonction L(x) de l'abscisse X1 à l'abscisse R1. Pour rappel, dans le cas des fonctions discrètes, l'intégration d'une fonction F(x) d'une abscisse a à une abscisse b peut être approchée par la méthode dites des rectangles (ou intégrale de Riemann), soit
11- Écrivez une première fonction personnalisée nommée calcul_A1 permettant l'intégration de la fonction L1(x) des abscisses X1 à Xi, avec une précision de 1 mm en abscisse (le pas d'intégration). [1 pt]
12- Écrivez une seconde fonction personnalisée nommée calcul_A2 permettant l'intégration de la fonction L2(x) des abscisses Xi à R1 dans les mêmes conditions de précision que pour L1(x) [1 pt]
Tous les éléments sont désormais mis en place pour résoudre le problème.
13- Résolvez définitivement le problème à l'aide du solveur en spécifiant bien vos cellules cibles et variables, et les conditions d'optimisation recherchées.
*** message déplacé ***


 autre en Bts
autre en Bts