Inscription / Connexion Nouveau Sujet
Probléme ouvert
Bonjour à tous 
j'ai un problème ouvert à faire et j'avoue ne pas vraiment comprendre la question 
Soient [AB] et [CD] deux segments fixés et parallèles ( non nécessairement de même longueur)
Où se trouve le lieu de tous les milieux des segments formés par des extrémités situées l'une sur [AB] et l'autre sur [CD] ?
Avez-vous une idée de la démarche que je dois effectuer pour trouver ce lieu et le démontrer ?
Merci d'avance 
Bonjour,
une première idée est de faire une conjecture (donc par exemple une figure dynamique avec Geogebra, ou quelques figures papier, ou imaginées dans sa tête)
ensuite cette conjecture il va falloir la démontrer
en gros c'est avec une histoire de droite des milieux / alias Thalès que tu vas prouver
- que tout milieu est sur un certain segment
- et que tout point de ce segment est un milieu possible.
J'ai fait une figure sur géogebra et je pense donc que le lieu des milieux est la droite où tous les milieux des segments se coupent et qui est parallèle aux deux autres mais je ne vois pas comment démontrer ma conjecture .
bof
l'idée pour faire une conjecture avec géogebra est déja de prendre deux segments pas aussi particuliers que ça
et donc déja de commencer par virer les axes de coordonnées et la grille et le magnétisme qui te fait mettre les points de préférence sur la grille
ensuite il est inutile de tracer autant de traits que ça !
un seul point M variable sur le segment [AB] et un seul point N variable sur le segment [CD]
construire le milieu I de MN
activer la trace de ce point I et balader M et N à volonté.
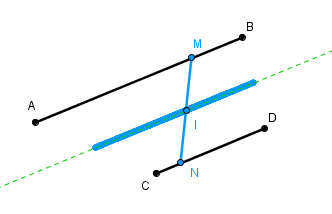
la droite
pour la démonstration :
si je te parle de la droite des milieux ça ne te dit rien ?
cette droite des milieux c'est à prendre avec
MN
MC et MD par exemple
tracer aussi AC et BD (enfin ceux qui rendent le quadrilatère obtenu convexe, peut être est ce AD et BC)
et les milieux de tous ces segments là.
(après tout ce sont des "cas" de positions de MN qui seront .. disons intéressants pour faire la démo)
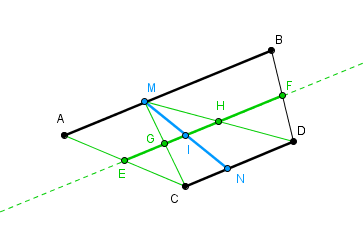
placer par contre des tas de positions sans aucune particularité n'offrira rien de bon pour la démonstration.
il faut prendre un seul MN et des droites particulières fixes (AC et BD disais-je) etc


