Quel est l'énoncé ?

slt, je bloque sur cette partie depuis environ 1 semaine pouvez-vous m'aider svp?
Je dois rechercher la position de M pour que le triangle BMC soit rectangle en M

1/Calculer BC²:

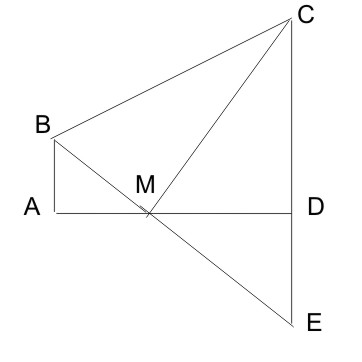
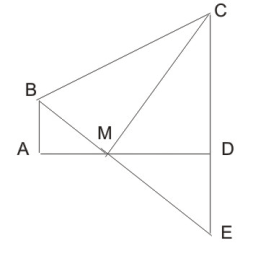
BA=2cm, AM=5.25cm, MD=1.75, CD=6cm, CM=6.25cm, AD=7cm de de plus les angles  et D sont droits.
PS= je sais que je dois utiliser le théorème de pythagore mais je ne sais pas comment    
trouver BM.
2/a) Exprimer BM² en fonction de x
  b) Exprimer CM² en fonction de x

3/ Quelle relation doivent vérifier ces trois précédentes longueurs au carré pour que BMC soit rectangle en M? L'écrire, la simplifier et montrer ainsi qu'on obtient 2x²-14x+24=0.

        merci!

                      



*** message déplacé ***

Bonjour,

Qu'est ce que x ?

*** message déplacé ***

slt, dans mon dm x=AM=5.25cm

*** message déplacé ***

J'imagine que x est une variable, donc comment as-tu trouvé x=5,25 ?

Quelles sont les données de ton énoncé ?

Toutes les cotes incluant le point M n'auraient pas du être données (sinon cela impose le point M et donc pas question de devoir chercher où le placer pour que triangle BMC soit rectangle en M).

Je renifle que AM = x

Pythagore dans le triangle ABM:
BM² = AB² + AM²
BM² = 4 + x²

Pythagore dans le triangle BMC:
MC² = MD² + CD²
MC² = (AD-AM)² + CD²
MC² = (7 - x)² + 6²
MC² = (7 - x)² + 36

Soit F le point de rencontre de la droite (CD) avec la parallèle à AD menée par B.

Pythagore dans le triangle BFC:
BC² = BF² + CF²
Or BF = AD = 7
et CF = CD - DF = CD - AB = 6 - 2 = 4
--> BC² = 7² + 4² = 65

Pythagore dans le triangle BMC:
BC² = BM² + MC²
65 = 4 + x² + (7-x)² + 36

x² + (7-x)² = 25
x² + 49 - 14x + x² = 25
2x² - 14x + 24 = 0

Et bingo.
-----

Bonjour Mdard !
Quand l'angle BMC est droit, les triangles BMA et MCD sont semblables : les angles BMA et MCD sont en effet égaux comme complémentaires au même angle MCD.
MA/CD = AB/DM.
Soit x = MA
x/6 = 2/(7-x)
En multipliant par 6*(7-x) : 7x-x² = 12; x²-7x = -12; x²-7x+12+0; multiplié par 2, cela correspond bien à l'équation que vous aviez annoncée.
Après avoir trouvé AM et MD, on peut calculer les côtés de l'angle droit, puis l'hypoténuse du triangle BMC.

Merci, pour votre aide

*** message déplacé ***

mdard,
il va falloir apprendre à répondre dans ton topic

Bonjour, je vous remercie encore pour votre aide qui me fut d'un grand secoure, mais j'ai encore un petit problème. Voila dans cette 3ème partie je recherche la position de M pour B, M et E soient alignés. On appelle E le symétrique de C par rapport à D.
1/Si B, M et E sont algnés, quelle configuration retrouve-t-on?
2/Calculer la valeur de x.
3/Justifier que cette position de M est celle pour laquelle CM+MB est minimal.
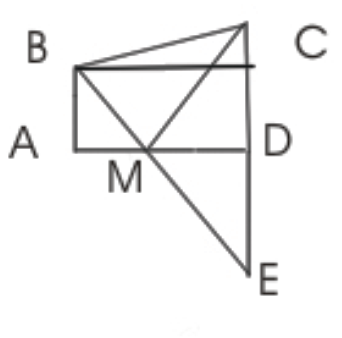
BA= 2cm, AM= 5.25cm, MD= 1.75, CD= 6cm, HD= 2cm, HC= 4cm, DE=6cm car DE est le symétrique de CD.
PS: je cnnais les réponse des 2 premières questions (je ne suis pas très sur du résultat de la deuxième question), en fait le pépin est pour moi: qu'est-ce que minimal?( Désolé de la qualité de la figure).
salut.



*** message déplacé ***

Bonjour,
Je n'ai pas suivi le début de cet exercice, mais peut-être que mes tuyaux t'aideront à avancer.
Si E est symétrique de C par rapport à D, que peux-tu dire de MC et ME ?
Que peux-tu dire de BM+MC et de BM+ME ?
Quel est le plus court chemin entre 2 points ?
Minimal signifie que tu ne peux pas trouver plus petit (pour une longueur plus court).
Bon courage pour finir.

*** message déplacé ***

    Bonjour. Dans cette situation, la longueur du segment BE est la plus petite possible.
    Je n'ai pas vu les exos qui précédaient.   J-L

*** message déplacé ***

    Bonjour Eve. Les grands esprits se rencontrent !
Désolé, je ne savais pas que vous répondiez .    J-L

*** message déplacé ***

Bonjour jacqlouis,
Pas de problème...
Je n'ai réclamé aucun monopole !
Cordialement.

*** message déplacé ***

moi oci je blok sur cette partie depui un bon bout de temps mais c'est cette dernière question qui me pose vraiment problème
pourriez vous maider?

la seule chose que je peux rajouter c'est l'énoncer du tout debut:

les angles A et D sont droits
AB= 2 cm
AD=7 cm
CD= 6 cm
M es tun point du segment AD tel que AM=x

c surtt sur ce dernier element que je voudrai dire quelqque chose pasque dans la partie 3 je trouve que x (donc AM) est egal a 1,75 ( je me suis peu etre trompé alor il fodrai verifier)
sil vou manque des infos nesiter pa a demander

paske je vois vraimt pas comen on pourai justifier que MC+MB est minimal

    J'avoue que je suis un peu perdu .... même dans le titre de l'exercice.

    Alors, si E est le symetrique de C, et si on suppose que les points B,M, et C sont alignés, on peut faire appel à Mr Thalès, pour calculer que,
puisqu'on a :  BA/AM = DE/MD  , on en tire : X = 14/8 = 1,75 .

  C'est la position de M qui correspond à l'alignement BME . Donc c'est pour cette position de M, donc pour cette valeur de x que la distance BME est minimale (la ligne droite étant le plus court chemin...).  
    Comme BME = BM + MC, cette valeur de x correspond bien à la valeur minimale de BM + MC.

    C'est bien cela que vous cherchiez ? Je ne suis pas très sûr ?   J-L

je vois ce que vous voulez dire mm si ce n'est pas encore très clair

parce que au debut je pensai kil existait un théorème ( une propriété) pour prouver cELA
mai si j'ai bien compri il faut juste faire des deductions

    Bonsoir Lise. Je t' ai dit mon incertitude, ne sachant plus quelle était (quelles étaient) la ou les questions posées.

    J'ai l'impression que j'ai à peu près bien répondu, sauf " que ce n'est pas encore très clair !". Donc c'est à améliorer, mais sur quel point ?
    Dis moi cela ?    J-L

la question que je posait etait " justifier que cette position de M est celle pour laquelle CM+MB est minimal" vous avez ( je crois ) repondu a cette kestion mais ce que vous m'avez repondu n'est pas encore très clair dans ma tête. Pouriez vous être plus précis ?

PS: dsl de ne pa avoir assez ciblée ma question dans mon premier message. En esperant que celui la sera plus clair pour que vous puissier maider.

    Bonsoir Lise. Si je me souviens bien , cet exercice nous faisait faire quelques calculs (Pythagore surtout) pour trouver la position de M , pour que l'angle(BMC) soit un angle droit.
    On a trouvé que pour cela, l'abscisse de M (x) sur AD devait être égale à 3 ou 4.

    Dans la partie 3°, on change de sujet. On laisse tomber cette valeur de M, et on passe à autre chose.
    On suppose que E est symétrique de C par rapport à D, et on demande quelle serait la nouvelle abscisse de M, si les points B, M, et E, étaient alignés. Dans cette configuration, on fait les calculs, en invoquant cette fois Thalès (chacun son tour !).

    Mais on constate, à cause de la symétrie, que ME est égal à MC. Donc si l'on nous demande de trouver la longueur minimale de (MB+MC), c'est comme si on demandait la longueur minimale de BE . La réponse est donc : cette longueur est égale à la longueur BM+ME puisque ces points sont alignés (la distance minimale entre les 2 points B et E étant forcément mesurée sur la droite BE).        C'est plus clair ? Je suis sûr que tu vas dire oui (?)  J-L

vous avez raison je vou repond OUI c plus clair . je vou remercie de votre aide et de votre patience.