Inscription / Connexion Nouveau Sujet
problème spé maths - graphes
Bonjour à tous, je ne comprends pas 2 questions de mon DM de spé maths à rendre dans 2 jours.
Voici l'énoncé :
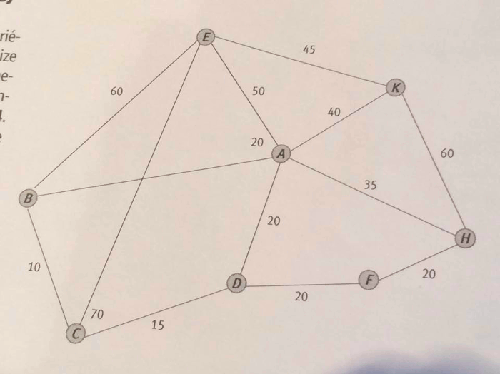
Ce graphe représente un parc boisé. L'entrée et la sortie du parc se font obligatoirement par le sommet E, les sept autres sommets représentant des carrefours. Le poids sur les arrêtes sont les longues, en dizaines de mètres, des allées reliant deux carrefours.
Je bloque à la troisième question : calculer la longueur minimale exprimée en mètres, de la promenade de Yann.
Merci de votre aide.
Cordialement.
Salut,
Va falloir se relever les manches et trouver la promenade la plus courte.
On va pas faire toutes les possibilités, parce que, par exemple, il est clair que faire E -> K -> H -> ... va forcément être un chemin plus long que E -> K -> A -> ...
Mais bon, essaye de voir les chemins qui sont susceptibles d'être les plus courts, calcul la longueur de ces chemins et conclut sur la longueur minimale.
Mais vu qu'il faut passé 2 fois par E (au début et à la fin) je ne sais pas comment faire avec le théorème de Dijkstra
A la limite tu peux créer un sommet S de sortie qui soit relié à B, A C et K avec la même pondération que pour E si ça te dérange trop.
fairegamee, est-ce que tu a réussi cette exercice? je suis en spé maths aussi et je dois envoyer cela rapidement mais je ne comprends pas de tout cet exercice!


