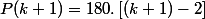Bonjour matlop,

Si j'ai bien compris, tu ne sais pas comment t'y prendre avec la récurrence.
Il faut commencer par se représenter ce à quoi pourrait ressembler un polygone à k+1 angles, et comment est ce que tu pourrais utiliser ta supposition (te ramener à un polygone à k angles).
Essaie de dessiner ton polygone avec des petites valeurs de k pour essayer de comprendre comment tu pourrais te ramener à ton hypothèse...

Si tu as encore du mal, je serai ravi de t'aider un peu plus...

Merci de votre réponse
Mais je ne sais toujours pas quoi faire
Comment je dois faire pour démontrer qu'elle est vraie au rang k+1, quels calculs faire?

Il faut que tu prennes un polygone à k+1 angles et que tu y découpes un triangle.
(je joins un dessin que j'ai fait sur Paint)

À partir de cela, tu peux dire que tu as un polygone à k angles et un triangle, alors tu sommes la valeur des angles.
D'après ton hypothèse de récurrence :
Tu ajoutes la somme des angles d'un triangle. (180°)
Tu as donc :


Tu devrais pouvoir conclure rapidement.

en voilà un qui a joué avec plusieurs comptes....
pas futé

Comment ça ?

il a ouvert plusieurs comptes ce qui est interdit et le site l'a banni...donc il s'est désinscrit
mais il a rouvert un nouveau compte, il devrait réapparaître sous un autre pseudo...attendons...

Bonjour, Fait-il calculer 180*(k+1-2)+180 ou juste 180*(k-2)+180?

je n?avais tout simplement pas reussi à récupérer mon ancien compte de seconde, j?ai tout simplement emprunté l?email de ma mère pour essayer de trouver de l?aide pour mon devoir. Je suis désolée si ça vous dérange mais je voudrais vraiment réussir

_{malou edit> ** vu ** retour aux maths maintenant **}

Tu mets juste en forme l'équation précédente pour bien comprendre que tu as démontré ton hérédité :

il est passé où le +180 de la première ligne? C'zst devenu le +1? si oui pourquoi ?

C'est une simple factorisation, il est devenu +1

Après avoir écrit tout ça donc:
P(k+1)=180*(k-2)+180
               =180*(k-2+1)
               =180[(k+1)-2]
               =180*(k-2)
Je conclue en disant que la propriété a été initialisée et est héréditaire et qu'elle est donc vraie?

La dernière ligne n'est pas bonne et l'avant-dernière est suffisante.

Une fois que tu as écrit l'avant-dernière ligne, tu peux écrire que ta propriété a été vérifiée pour k+1, avec k vraie donc la propriété est bien héréditaire.



Tu n'as plus qu'à conclure.

la dernière ligne est donc:
180*(-k-1)??
si c'est cela ça veut dire qu'elle n'est pas héréditaire puisque j'étais censée trouver             180*(k-2)

Non, tu es sensé montrer que c'est vrai pour k+1 donc que

C'est ce qu'on vient de faire

donc je m'arrête à la ligne:

?*