Inscription / Connexion Nouveau Sujet
Problème sur les angles orientés
Bonjour à tous!
Voilà, j'ai des difficultés à résoudre un exercice sur les angles orientés. J'ai beau chercher, je ne trouve rien. J'espère donc trouver de l'aide sur ce forum. Voici l'énoncé:
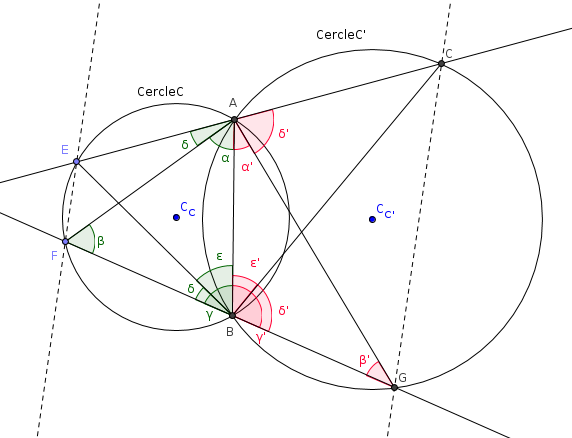
a) On appelle (C) et (C') deux cercles de rayons quelconques et sécants en deux points A et B. On trace une droite passant par A et coupant les deux cercles. Elle coupe(C) en E et (C') en C. De même, on trace une droite passant par B et coupant les deux cercles. Elle coupe (C) en F et (C') en G.
Démontrer que les droites (EF) et (CG) sont parallèles.
b) On appelle (C) et (C') deux cercles de rayons quelconques et sécants en deux points C et I. On trace un troisième cercle (C'') passant par I et sécant aux deux premiers cercles. (C'') coupe (C) en B et (C') en A. On trace une droite passant par C et coupant les deux cercles (C) et (C') respectivement en M et M'. De même, on trace une droite passant par A et par M'. Elle coupe (C'') au point M''.
Démontrer que les points B, M et M'' sont alignés
Merci d'avance à tous
PS: Ces exercices sont difficiles 
Non, EFB n'est pas forcément un triangle rectangle car rien ne prouve que le centre du cercle (C) et et les points E et B sont alignés.
PS: Du moins, pour ma part 
oui, c'est vrai.
la propriété fondamentale est qu'un segment sur un cercle est vu sous un angle constant par tous les points de l'arc de cercle limité par ce segment.
Il faut décomposer les angles élémentaires pour montrer que BFE + BGC forme un angle plat, ce qui impose alors que (FE) et (CG) sont //
Je ne vois pas trop comment "décomposer les angles élémentaires". Pourrais-tu m'éclairer un peu s'il-te-plaît?
Tiens, il y a beaucoup plus simple, si on utilise une autre propriété que tu vas pouvoir me rappeler :
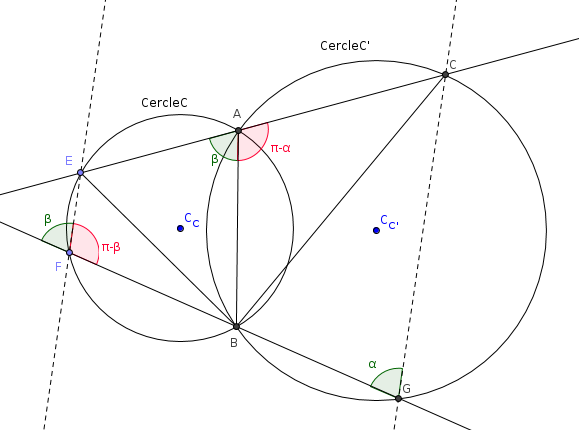
Si je comprends bien, il faut que je trouve une relation entre tous ces angles élémentaires afin que j'aie: ( ,
, )+(
)+( ,
, )=
)= ?
?
D'accord:
Comme  +(
+( -
- )=
)= ,
,
alors -
- =0 et
=0 et  =
=
Mais ce que je ne comprends pas c'est ta figure. Pourquoi est-ce que BAC= -
- ? et pourquoi est-ce que BFE=
? et pourquoi est-ce que BFE= -
- ?
?
C'est justement la propriété dont je te parlais
si on utilise une autre propriété que tu vas pouvoir me rappeler
J'espérais que tu allais me la donner. Quelle déception...
Un petit effort de mémoire ? ou de recherche ?
En fait, aucune propriété de mon cours ne m'interpelle pour ce cas de figure...
J'opterais bien pour la recherche, mais où chercher?
wikipédia, wikiversité
ce ne sont pas les sources d'information qui manquent.
cherche cercle et angles inscrits
Il faut tracer les diamètres des cercles (C) et (C') tels que les points A et F d''une part et C et G d'autre part soient diamétralement opposés. Suis-je sur la bonne voie?
non
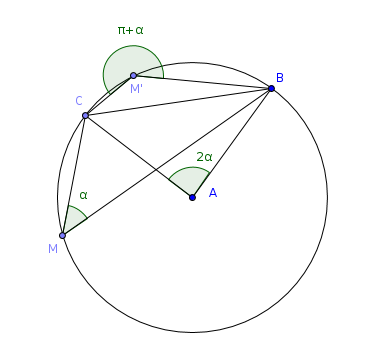
Soit un cercle de centre A, et [BC] une corde de ce cercle qui ne passe pas par A
Soit M un point de l'arc de cercle situé dans le même demi plan que A par rapport à la droite (BC)
Soit M' un point de l'arc de cercle complémentaire
alors
Alors il est facile de montrer que l'on a aussi
Voilà la propriété que j'ai utilisée pour résoudre ton exercice.
Si la corde passe par A, c'est à dire si elle est un diamètre, alors
Bonsoir dhalte,
Tout d'abord je m'excuse vraiment de tout le temps que j'ai mis pour te répondre, je ne retrouvais pas le topic...
Pour résoudre le deuxième exercice, j'ai utilisé la même propriété que tu as évoquée plus haut...
Suis-je sur la bonne voie? Je pense avoir réussi.
Effectivement, ça fait un mois que j'attends anxieusement la suite...
Suis-je sur la bonne voie ?
tu es sur la bonne voie
Je pense avoir réussi
Je te félicite