Inscription / Connexion Nouveau Sujet
probleme sur pythagore pour lundi
Voila l'exercice:
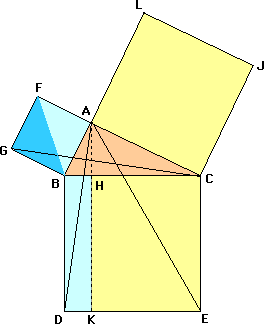
ABC est un triangle rectangle en A. ABGF, ACJL et BCED sont des carrés. La droite (AH) est perpendiculaire à (BC).
1a. Justifier que (BG)//(FC). Demontrer que ds le triangle GCB, la hauteur issue de C a pour longueur AB. En déduire que GBA et GBC ont la meme aire.
b. Comparer les angles GBC et ABD. En déduire que les triangles GBC et ABD ont la meme aire.
c. Démontrer que les triangles ABD et HBD ont la meme aire.
d. En déduire que le carré ABGF a la meme aire que le rectangle BHKD.
2. Pour le meme raisonnement on démontre que l'aire du carré ACJL est égale a celle du rectangle CHKE.
3. Conclure
Merci d'avance
Le but du forum n'est pas de faire ton exercice mais de t'aider à le faire. Indique nous ce que tu as réussi à faire .
J'ai réussi à démontrer que (BG)//(FC) et c'est tout.
1) a) car BGFA est un carré. De la même manière
. Or on sait également que
du fait que le triangle ABC soit rectangle en A. Les points F,A et C sont donc alignés. Dans le carré GBAF, (GB)//(FA), par conséquent
je n'ai toujours pas trouver la solution.je n'ai rien trouvé d'autre. C'est à rendre pour demain alors svp aidez moi.
bonjour à tous, j'ai un exercice à faire pour demain et je n'y arrive pas pouvez vous m'aider
Voila l'exercice:
ABC est un triangle rectangle en A. ABGF, ACJL et BCED sont des carrés. La droite (AH) est perpendiculaire à (BC).
1a. Justifier que (BG)//(FC). Demontrer que ds le triangle GCB, la hauteur issue de C a pour longueur AB. En déduire que GBA et GBC ont la meme aire.
b. Comparer les angles GBC et ABD. En déduire que les triangles GBC et ABD ont la meme aire.
c. Démontrer que les triangles ABD et HBD ont la meme aire.
d. En déduire que le carré ABGF a la meme aire que le rectangle BHKD.
2. Pour le meme raisonnement on démontre que l'aire du carré ACJL est égale a celle du rectangle CHKE.
3. Conclure
J'ai réussi à faire la question 1a.:
[BG]perpendiculaire à [BA]car BGFA est un carré.
De meme [AF] perpendiculaire à [BA]
Or[AC] perpendiculaire à [BA] car ABC est un triangle rectangle en A.
Les points F A C sont alignés. Dans le carré GBAF, (FA)//(GB).Dc (GB)//(FC)
Merci d'avance
** image supprimée **
*** message déplacé ***
Salut
1-b
BA=BG on se place dans le carré BAFG
BD=BC on se place dans le carré CBDE
Ensuite tu considères une rotation de centre B et d'angle 90°
elle transforme D en C
elle transforme A en G
elle transforme donc (DA) en (CG)
d'ou DA=CG
Les deux triangles sont donc identiques (similaire si je me souviens bien du vocabulaire ... mais a confirmer) et ont donc la même aire.
*** message déplacé ***
1-c
La formule de l'aire d'un triangle est A =0.5*Base*Hauteur
ABD et HBD ont la même base
La hauteur issue de A du triangle ABD est égale à BH, hauteur du triangle BHD.
Ces deux triangles ont donc la même aire ...
attention, ma rédaction n'est pas très "mathématiques" (lol) a toi de l'améliorer, tu as déja le principe
*** message déplacé ***
désolé je n'ai pas le temps de t'aider pour la suite
bon courage
boris
*** message déplacé ***
1)
a)
angle(FAB) = 90°
angle(BAC) = 90°
angle(FAC) = angle(FAB) + angle(BAC)
angle(FAC) = 90° + 90° = 180°
Et donc les point F,A et C sont alignés.
Comme (BG) est // (FA) (puisque ABGF est un carré), on a (BG) // (FC)
---
On prolonge [GB] au delà de B et on trace la // à AB passant par C.
Ces 2 droites se renontre en un point M.
Le quadrilatère ACMB est un rectangle (cotés opposés // et angles droits).
[MC] est la hauteur issue de C du triangle BGC, or |MC|=|AB|
-> La hauteur issue de C du triangle BGC a pour longueur AB
---
Aire(GBC) = (1/2).GB.hauteur issue de C
Aire(GBC) = (1/2).GB.AB
Aire(GBA) = (1/2).CB.AB
-> Aire(GBC) = Aire(GBA)
-----
b)
Les angles GBC et ABD ont leur cotés perpendiculaires et les 2 angles sont obtus.
-> Les angles GBC et ABD sont égaux
Comme on a aussi: GB = BA et BC = BD, les triangles GBC et ABD sont isométriques (un angle et les cotés adjacents égaux).
-> les triangles GBC et ABD ont la meme aire.
-----
c)
Aire(HBD) = (1/2).BD.BH
Si on prolonge [DB] au delà de B et que l'on trace la // à BH passant par A.
Soit N le point de rencontre de ces 2 droites.
Le quadrilatère BHAN est un rectangle.
-> BH = AN et comme BH est perpendiculaire à BD et BH // AN, on a AN perpendiculaire à (DB).
Et donc AN est la hauteur issue de A du triangle ABD.
Aire(ABD) = (1/2).BD.AN, et comme BH = AN ->
Aire(ABD) = (1/2).BD.BH
--> Aire(HBD) = Aire(ABD)
-----
d)
On a montré que:
Aire(GBC) = Aire(GBA)
Aire(GBC) = Aire(ABD)
Aire(HBD) = Aire(ABD)
-> Aire(GBA) = Aire(HBD)
2*Aire(GBA) = 2*Aire(HBD)
Aire(ABGF) = Aire(BHKD)
-----
2)
Par le même raisonnement on démontre que l'aire du carré ACJL est égale a celle du rectangle CHKE.
-----
3)
Des 2 points précédents,on a prouvé que:
Aire(ABGF) = Aire(BHKD)
Aire(ACJL) = Aire(CHKE)
En ajoutant ces 2 égalités membres à membres ->
Aire(ABGF) + Aire(ACJL) = Aire(BHKD) + Aire(CHKE)
Aire(ABGF) + Aire(ACJL) = Aire(BCED)
-----
Sauf distraction. 
*** message déplacé ***



