Inscription / Connexion Nouveau Sujet
Produit scalaire
Bonjour j'ai un exercice que je comprends pas bien
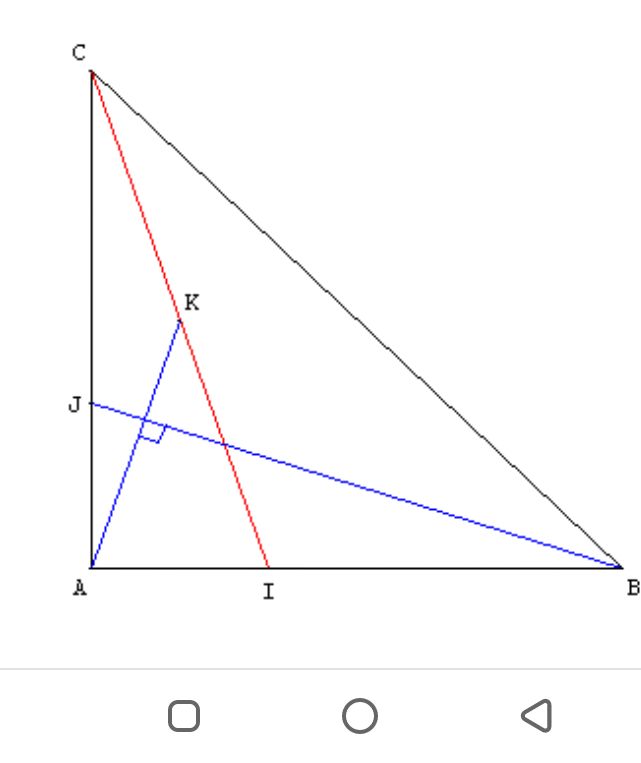
Soit ABC un triangle rectangle isocèle en A.
Soit I le point de [AB] tel que AI = AB/3 ;
J le point de [AC] tel que AJ = AC/3 ; et K le milieu de [IC].
Démontrer que les droites (AK) et (JB) sont perpendiculaires.
Bonjour à tous,
@Asata,
Tu as posté un autre sujet similaire pour lequel tu as eu des réponses.
Suivies d'un silence radio assourdissant...
La bienséance voudrait que tu répondes dans le premier sujet avant d'en poster un autre.
Avec la relation de Chasles j'ai trouvé AK=AI+IK et JB=JA+AB mais je suis bloqué je n'arrive pas à faire la suite
JB = JA + AB te servirsa.
Quant à AK, ce n'est pas suffisant . Il faudrait que tu le décompose aussi suivant des vecturs portés par les côtés de l'angle droit du triangle ABC.
Je ne comprends toujours rien hein bon On sait que AK=AC+CK et JB=JA+AB mais comment trouver un lien entre AK et JB pour que le produit scalaire AK.JB=0
tu veux montrer que les droites (AK) et (BJ) sont perpendiculaires ...
que te suffit-il de démontrer pour avoir cela ?
ben voila !!!
et cela change-t-il si on calcule le produit scalaire 2AK.JB ?
il suffit alors de reprendre ce que tu as trouvé pour JB et 2AK ...
Bonsoir
On a d'abord JB=JA.+AB ET AK=1/2AC+1/2AI
j'ai ensuite calculé le produit scalaire AK.JB ce qui donne AK.JB=1/2AC.JA+1/2AC.AB+1/2AI.JA+1/2AI.AB=1/2AC.JA+1/2AI.AB or on sait que AI=1/3AB comment le triangle est rectangle isocèle alors AB=AC et AJ=1/3AC=1/3AB on n'a donc 1/2AC.JA=1/2×(-1)AB×1/3AB=-1/6AB² car les vecteur AC JA sont de sens opposé
1/2AI.AB=1/2×1/3×AB×AB=1/6AB²
et on conclure
comme je l'ai dit calculer le produit scalaire 2AK.JB est suffisant puisque 2 * 0 = 0 et évite d'alourdir les expressions avec des coefficients 1/2 ...
Bonjour
et même le coefficient 1/3 peut être éliminé
en effet il suffit juste d'écrire en littéral que AB = AC et AI = AJ
et donc
ouvrant la voie à une généralisation du problème à un triangle rectangle quelconque et des points I et J tels que AI et AJ soient inversement proportionnels aux côtés :
quelconque.
nota (ça fait mal aux yeux, et même modifie le sens) :
comme le triangle ... on a donc ... on conclut


