Inscription / Connexion Nouveau Sujet
Produit scalaire espace
Bonjour,
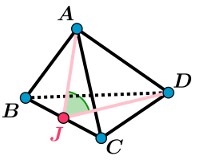
ABCD est un tétraèdre régulier de côté a.
J est le milieu de [BC].
Déterminer une mesure de l'angle AJD à 0.1° près.
a)
Les faces sont des triangles équilatéraux et les angles mesurent 60°.
(JA) et (JD) sont des hauteurs et JA et JD mesurent chacun a*Racine(3)/2.
JA.JD=( a*Racine(3)/2)²*cos(AJD)=3*a²/4*cos(AJD).
b) JA.JD=(JB+BA).JD=JB.JD+BA.JD mais Ba et JD ne sont pas dans le même plan.
J'ai essayé d'autres compositions mais je tourne en rond !
La méthode c'est d'avoir les vecteurs dans le même plan.
Merci d'avance.
Merci pour ta réponse.
Je me suis penché sur le double produit scalaire et la relation de Chasles pour tourner en rond.
Alors, JA=Jd=a*Racine(3)/2
Théorème d'Al-Kashi:
AD²=JA²+JD²-2JA*JD*cos(AJD).
Application: cos(AJD)=1/3
donc l'angle AJD=70,5°
J'èspère que je n'ai pas fait d'erreur de calcul
Bonsoir,
Cela me paraît juste.
Mais, dans ce calcul, il n'y a pas de produit scalaire, contrairement à ce qu'annonçait le titre . . . .
Bonsoir Priam,
Al-Kashi se retrouve facilement à partir de la notion de produit scalaire. C'est du moins ainsi qu'on le démontrait en première quand j'étais en fonction. 
Oui, cet exercice est dans le chapitre "produit scalaire dans l'espace".
C'est pour ça que j'ai voulu le faire en calculant de deux façons le produit scalaire mais je n'ai pas pu faire la deuxième façon, je tournais en rond (voir mon premier message).
Il est possible de calculer l'angle JDA en écrivant de deux manières différentes le produit scalaire DJ.DI , I étant le milieu de AD.
Non, c'est bien l'angle JDA; la valeur de l'angle DJA s'en déduit immédiatement.
Comment écrire le produit scalaire DI.DJ ? Il y a la formule classique avec cosinus, et une autre façon . . .
Bon, DJ.DI=DJ*DI*cos(JDI), calcul simple.
Par décomposition de DI et DJ:
DI.DJ=DI.(DC+CJ)=DI.DC+DI.CJ , le problème DI et CJ ne sont pas dans la même plan.
J'ai essayé d'autres décompositions et c'est toujours le même problème!
Le produit scalaire DJ.DI peut ainsi s'écrire DJ*DI*cos(JDI).
Mais il peut se mettre sous une autre forme (par projection orthogonale).
Je conjecture: le projeté orthogonal de J sur [DA] est I.
DJ=a*Racine(3)/2
DI.DJ=DI²
DI=a/2
DJ*DI*cos(JDI)=DI²
Finalement cos(JDI)=1/Racine(3)
JDI=54,7°
Le tiangle AJD isocèle en J.
AJD=70,5° c'est le résultat que j'ai trouvé en utilisant Al-Kashi.
Mais faut-il démontrer la conjecture que j'ai émise ou bien ça découle du fait que ABCD est régulier ?
D'accord.
Pour le projeté de J, c'est mieux qu'une conjecture, étant donné que le triangle AJD est isocèle en J et que I est le milieu de son côté AD.


