Inscription / Connexion Nouveau Sujet
Profondeur d'un puits : DM
Bonjour,
dans un exercice de mon DM il faut calculer la profondeur d'un puits de la même manière qu'un arpenteur dans l'antiquité :
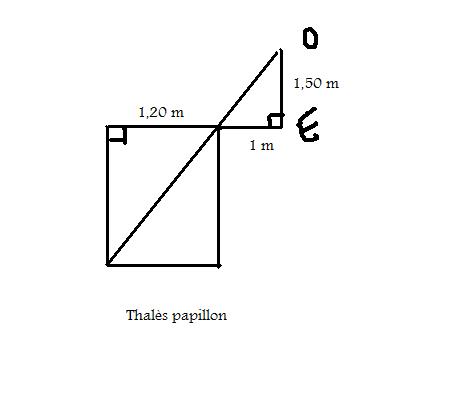
Lucas a décidé d'employer cette méthode pour mesurer la profondeur d'un puits de 1,20m de diamètre. Il se place à env. 1m du bord du puits et aligne son oeil, situé à 1,50m de hauteur avec le bord de celui-ci et le coin opposé du fond.
a) Faire un schéma de la situation.
b)En déduire la profondeur du puits.
Pour le b) j'ai compris qu'il fallait utiliser le théorème de Thalès mais je n'arrive pas à prouver que la droite qui fait 1m et celle du fond du puits son parallèle.
En espérant que vous m'avez compris... 
Merci d'avance
D'accord mais comment fait-on pour mettre un schéma fait sur open office en format jpg ou autre.
Merci
S'il vous-plaît dites-moi comment on fait le schéma ou du moins sur quel site (OpenOffice...) :/
Merci beaucoup d'avance
Bonjour,
merci pour ton schéma 
, mais moi il n'est pas indiqué que le triangle du dessus est rectangle, ni que le puits soit rectangle...
Moi ce que j'aimerais savoir c'est comment prouver que le fond du puits et la base du petit rectangle sont parallèles...
Merci d'avance,
Cordialement
Si on a un dessin , on doit voir le symbole de l' angle droit .
Sinon , l' énoncé devrait parler de " perpendiculaire à ... "
Si on n' a rien dans un sens ou dans un autre , on ne peut
pas résoudre car on applique le théorème de Thalès
que si les droites sont parallèles .
Bonjour,
Dans un énoncé, il y a des éléments du message qui sont implicites. C'est-à-dire qu'il est inutile de préciser :
- "Bobby est rentré !"
ou
- "Elle a perdu son porte-monnaie."
D'abord, ce garçon (Bobby) est arrivé. Mais
ça pourrait être un chien !
Puis, elle a perdu son argent. Mais si ce porte-monnaie
était vide, elle n'a perdu que le contenant de la monnaie.
Tu vois que dans la plupart des discours, on se base sur ce qui sera compris par la majorité des gens.
Si le petit triangle est rectangle, c'est qu'on suppose
que Lucas va bien (que sa position est dans un axe bien VERTICAL). Et que le sol, à proximité, n'est pas défoncé (qu'il est HORIZONTAL).
Si le puits ne ressemble pas à un rectangle (vu "de profil"), que les parois sont 'tordues', même si cela arrive, ce genre de puits ne sera JAMAIS proposé comme
problème.
Les mathématiques raisonnent sur des formes idéales. C'est pour ça qu'elles sont abstraites.
Et donc, on invite l'élève à admettre comme Fond du Puits, une largeur bien droite, et bien HORIZONTALE.
Annuler
connectez vous