Inscription / Connexion Nouveau Sujet
pyramide
bonjour aidez moi s il vous plait!
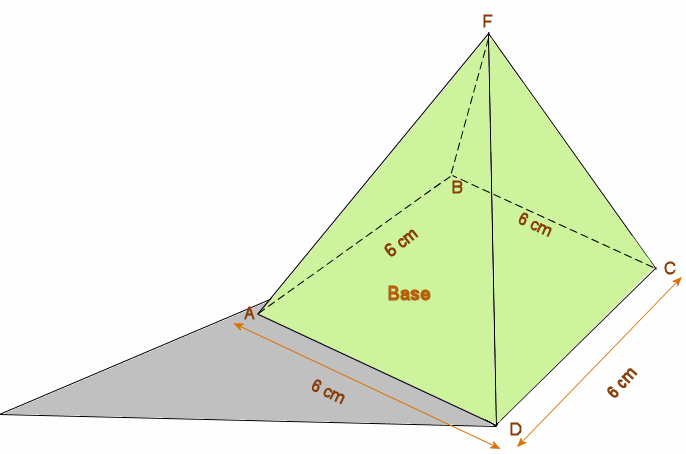
on veut couper une pyramide régulière dont la base est un carré de coté 6cm et et la hauteur est 4cm parallèlement a la base. a quelle distance du sommet doit on coupe cette pyramide pour que les 2 parties est le même volume??
expliquer clairement les étapes de votre raisonnement( s il vous plait)
j'ai calculer le volume de la pyramide ensuite j'ai diviser le volume par 2
V=(1/3)*H*A
= (1/3)*4*(6*6)
V = 48 cm²
on a ensuite pour que les 2 parties aient le même volume il faut que V1=V2 c.a.d V = V1 + V2
donc V1 = 24
or une partie est une petite pyramide et l autre est un parallélépipède non rectangle
pour la petite pyramide la base est aussi un carré mais de dimension inconnue et pour le parallélépipède on a juste l'aire de base inchangée voila ou j en suis .
Bonsoir,
quand on multiplie les dimensions d'un solide par un nombre a, le volume est multiplié par a3.
La petite pyramide est obtenue en multipliant les dimensions de la pyramide de départ par un certain réel inconnu. (Thalès)
Son volume est la moitié de celui de la pyramide de départ.
Je te laisse conclure...
Bonsoir.
En notant par le demi-côté de la base et par
la hauteur de la pyramide initiale et par b et h les éléments analogues de la petite pyramise obtenue, on aura alors
d'où
Mais on a où \alpha est l'angle formé par la hauteur de pyramide et la hauteur issue du somment de la pyramide (c'est le même pour les pyramides).
et
d'où
et finalement
. on en déduit
Remarque Si , on trouve rapidement
et
.
Pour l'exemple donné cm et donc
cm
Bonsoir.
Verdurin a été plus rapide que moi de même pour sa méthode. La manière de découper la pyramide donne deux pyramides semblables.
@Delta-B
Slt jai reflechi pendant pratiquement 2/4 heure sans toute fois comprendre ceci ( \dfrac{a}{H}=\dfrac{b}{h} = c = tan(\alpha)
Bonjour.
@force-tranquille
Exact!
Désolé! Il manquait (omission de mots) ".....d'une face...." ce qui rendait la phrase et la formule incompréhensibles.
Mais on a où \alpha est l'angle formé par la hauteur de la pyramide et la hauteur d'une face (apothème) issue du somment de la pyramide (c'est le même pour les 2 pyramides). Le figure est plus explicite,
S : sommet de la pyramide, O: centre de base, M milieu d'un coté de la base de la pyramide initiale.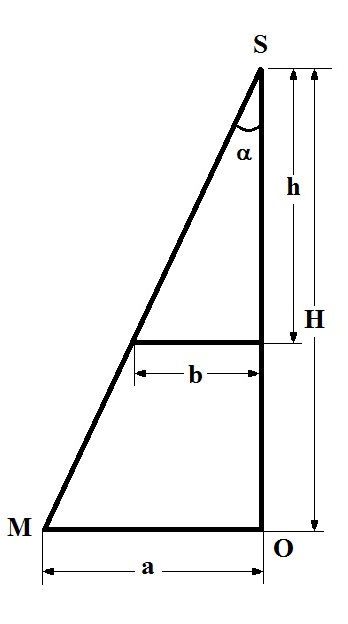

(Le triangle se trouve dans le plan passant par le sommet de la pyramide les milieux de 2 côtés opposés de base.)


 géométrie en post-bac
géométrie en post-bac