Inscription / Connexion Nouveau Sujet
Pyramide
Bonjour à tous,
j'ai fait un PB mais je voudrais savoir si il est juste. Merci de m'aider.
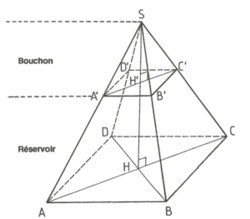
Une lampe diffuseur de parfum a la forme d'une pyramide régulière SABCD de base carrée.Ses arêtes latérales mesurent 14,7 cm et le côté de la base mesure 12 cm. 1)Calculer la longueur de la diagonale DB du carré: Pythagore dans le triangle ABD DB2=AB2+AD2
DB=12 2=16,97 cm.2)Montrer par le calcul qu'une valeur approchée au cm près, de la mesure de la hauteur de la pyramide SABCD est 12 cm: Pythagore dans le triangle SHB SB2=SH2+HB2 SH=
2=16,97 cm.2)Montrer par le calcul qu'une valeur approchée au cm près, de la mesure de la hauteur de la pyramide SABCD est 12 cm: Pythagore dans le triangle SHB SB2=SH2+HB2 SH= 144 =12 cm.3)Calculer le volume de la pyramide SABCD:Aire du carréABCD=144cm2 donc
144 =12 cm.3)Calculer le volume de la pyramide SABCD:Aire du carréABCD=144cm2 donc
V SABCD=144*12/3=576 cm3.4)La partie supérieure SA'B'C'D'qui abrite le bouchon est une réduction de la pyramide SABCD.Sa hauteur est 1/4 de la hauteur de SABCD.Calculer son volume:SH'=3 cm car 12cm/3cm, Thalès dans SH'C' et SHC donc SC'=3,675cm et H'C'=2,12 cm. Considérons Pythagore pour H'C'B donc B'C'2=H'C'2+H'B'2 B'C'=3cm donc V SA'B'C'D'=10 cm3.5)La partie inférieure sert de réservoir au liquide parfumé.Calculer le volume de liquide que peut contenir la lampe: V SABCD-V SA'B'C'D'=566 cm3 ou 0,566 litres ou 56,6 dcl.
Merci pour votre aide j'espère que ce n'est pas trop long

Bonjour,
Ton message est très difficile à lire. Cela n'incite pas à s'y plonger.
Ta réponse à 2) est fausse.
Bonsoir à tous,
Merci qu'en même d'avoir essayé je me doutais bien que ça allait faire trop long.
Merci d'avoir répondu à la question 2

Le problème n'est pas sa longueur, mais sa présentation difficile à lire.
Suite à nos remarques ci-dessus, tu aurais pu corriger la suite, qui est fausse. 
SH = (3/10)V1601
3) Volume de la grande pyramide :
V(SABCD) = (1/3).SH.A(ABCD) = (1/3).(3/10)(V1601).144 = (72/5)V1601 environ 576,18 cm3 (et pas égale 576)
4) Volume de la petite pyramide :
SH' = SH/4 = (3/40)*V1601 environ 3 cm (et pas égale !)
H'C' = (1/4)HC = (1/4)6V2 = (3/2)V2 environ 2,12 cm (et pas égale !)
B'C' = 3 cm
V(SA'B'C'D') = (1/3).SH'.A(A'B'C'D') = (1/3).(3/40)*(V1601).9 = (9/40)V1601 environ 9 cm3 (et non pas égale 10 !!!!)
Vérifions en remarquant que la petite pyramide est la grande, dont les dimensions ont été divisées par 4. Donc le volume est divisé par 4^3 :
V(SA'B'C'D') = V(SABCD)/4^3 = (72/5)*(V1601)/64 = (9/40)V1601
On retrouve bien le même résultat.
Sauf erreur.
Nicolas
Bonjour Nicolas,
Désolé, mais je n'ai pas osé poursuivre le PB.
C'est pour cela que je te remerciais pour ton aide et quittais le forum.
En tout cas, je tacherais à l'avenir d'avoir une présentation plus lisible.
Je te remercie pour ta patience et ta gentillesse pour avoir qu'en même vérifié mon devoir.
A bientôt bonne journée!







 géométrie en post-bac
géométrie en post-bac