Inscription / Connexion Nouveau Sujet
pyramide
Bonjour, voila mon pb:
pour la 1) je dis d'apres thales SM/SA = SN/SB=MN/AB = 1/3
donc MN/AB=1/3 et MN = 1/3 (AB)
alpha= MN^2 =(1/3 (AB)^2) = (1/9) *AB^2 = (1/9) * beta
est ce correct?
2) aucune idée
Merci 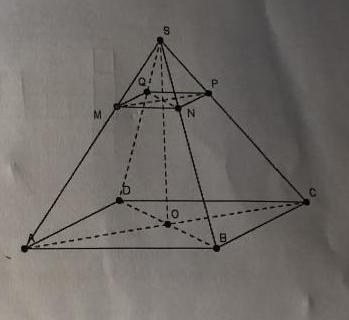
malou > **image recadrée sur la figure conformément à ![]() Sujet ancien- ne plus donner ce lien-merci***point 3****
Sujet ancien- ne plus donner ce lien-merci***point 3****
Donc dsl pour l'image..A supprimer je ne peux pas le faire
voici le pb : 1
2 pyramides regulieres l'une dans l'autre.
sommet S
base de la petite MNPQ
Base de la grande ABCD et milieu O.
On a SM=1/3 de SA SN = 1/3 de SB etc..
alpha = aire de MNPQ
beta = aire de ABCD
Question 1 montrer que alpha = (1/9 )* beta
je dis d'apres thales SM/SA = SN/SB=MN/AB = 1/3
donc MN/AB=1/3 et MN = 1/3 (AB)
alpha= MN^2 =(1/3 (AB)^2) = (1/9) *AB^2 = (1/9) * beta
est ce correct?
Question 2
en deduire le volume de lapyramide SMNPQ en fonction de SABCD
Je vois pas ..
Merci!!
Tu n'as pas la hauteur, mais tu peux utiliser Thales pour trouver une relation entre les hauteurs h et H des deux pyramides.
Avec R l'intersection des diagonales du petit carré, on peut utiliser Thalès dans un triangle de côté SO .
Oui, on peut appliquer Thalès.
A condition de démontrer avant (MR)  (AO) .
(AO) .
Pour cela, on peut utiliser la réciproque de Thalès dans le triangle ASC .
ok :
v1 volume petite pyramide
v2 volume grande pyramide
SR/SO = SM/SA = MR/AO
et
V1= (MN^2 * SR) / 3 = alpha * SR /3
V2= (AB^2 * SO) /3 = 9 *alpha *SO /3 car beta = 9 alpha
donc
alpha = (3* V2) / (9 * SO)
et V1= ((3*V2/9*SO) *SR )/ 3 = V2 * (SR/SO) = V2 * (SM/SA) = V2/3
c'est ça ?!
Regarde ta figure, as-tu l'impression que le volume de la petite pyramide est le tiers de la grande ?
SO = H et SR = h . Quel est le rapport entre H et h ?
Ecrire ensuite V1 = 
 h / 3 = (
h / 3 = ( / 9)
/ 9)  (h / 3) = ...
(h / 3) = ...
h=H/3
V2=Beta * H/3
V1= (beta * h) /27 = (3*V2 *h) /(27*H)=(3*V2 * H)/(3*27*H) = V2/27
c'est mieux ?!
Oui, c'est bon.
Mais je ne vois pas d'où vient V1= (beta * h) /27 au départ de ton calcul de V1 .
Ecrit avec de vraies fractions :
De rien, et d'accord pour "V1 = (alpha * h) / 3 or alpha = beta /9 donc V1= beta * h /27"
A partir de là, c'est encore plus rapide que dans mon message :
V1 = beta * h /27 = (beta*(H/3)) / 27 = V2 / 27 


