Inscription / Connexion Nouveau Sujet
pythagore
Bonsoir voici un DM merci de m'aider
Voici l'enoncer:
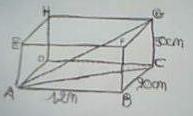
La fiqure si dessous represente un parallelepipede rectangle de longueur 1.2m de largeur 90cm et de hauteur 50cm
1.Quelle et la nature de laface ABCD
calculer la longueur de Ac
2.Quelle est la nature du triangle ACG ? Calculer la longueur de AG,arrondie au dixieme ,d'une diagonale du parallelepipede rectangle.
bonsoir
1°Soit le triangle rectangle ABC
AC²=AB²+BC²
2° [CG] perpendiculaire à [AC]
Alors le triangle ACG est rectangle en C
Salut,
kenavo27 a appliqué le théorème de Pythagore :
Sur ta figure, on voit clairement que ABCD est un rectange et [AC] une diagonale qui divise ton rectangle en deux triangles rectange. On remarque alors que [AC] est l'hypothénuse des deux triangles rectangle, donc tu utilise la formule qu'à écrit kenavo27 :
AC²=(12)2+(90.10-2)2 => Attention aux unités car BC est en centimètres
AC²=144 + 0,81
AC²=116,64
AC==10,8 m
Désolé, je me suis planté royalement loool
Le segment sensé être le plus long est plus court qu'un autre sensé être moins long...
Je croit que je suis fatigué là, je vais me coucher 
Désolé d'avoir perturbé la recherche...
Re bonsoir,
J'ai mal vu :
[AB] n'est pas égal à 12m mais 1,2m... A daccord xD
AC²=(1,2)2+(90.10-2)2
AC²=2,25
AC==1,5 m
ça à l'air plus coérent là non ? 
Bonne soirée
Bonjour sysyem2 je n'ai pas compris comment tu a calculer que AC²=(1,2)2+(90.10-2)2
=2.25
merci de me repondre
Bonjour fatma59
system32 a mis les longueurs en mètres 90 cm=90*10 puissance - 2, c'est à dire divisé par 100,
soit 0,9 m (10 puissance -2=1/100)
et AC²=1,2²+0,9²=1,44+0,81=2,25
On pouvait aussi tout mettre en cm et diviser le résultat final par 100 si on veut l'avoir en mètres
Bonsoir voici un DM merci de m'aider
Voici l'enoncer:
La fiqure si dessous represente un parallelepipede rectangle de longueur 1.2m de largeur 90cm et de hauteur 50cm
1.Quelle et la nature de laface ABCD
calculer la longueur de Ac
2.Quelle est la nature du triangle ACG ? Calculer la longueur de AG,arrondie au dixieme ,d'une diagonale du parallelepipede rectangle.

1) c'est un rectangle
Calculer AC :
(1,2m = 120 cm)
Dans le triangle ABC rectangle en B
D'après le théorème de Pythagore on a :
AC² = BA² + BC²
AC² = 120² + 90²
AC² = 14400 + 8100 = 22500
AC² = √22500 = 150
Donc AC = 150 cm / 1,5m
1) c'est un rectangle
Calculer AC :
(1,2m = 120 cm)
Dans le triangle ABC rectangle en B
D'après le théorème de Pythagore on a :
AC² = BA² + BC²
AC² = 120² + 90²
AC² = 14400 + 8100 = 22500
AC[strike][/strike] = √22500 = 150
Donc AC = 150 cm / 1,5m
2) la JSP
Dans le triangle ACG rectangle en C
D'après le théorème de Pythagore on a :
AG² = AC² + CG²
AG² = 150² + 50²
AG² = 22500 + 2500 = 25000
AG = √25000 ≈ 158, 1



