Inscription / Connexion Nouveau Sujet
Pythagore, triangle equilateral
Bonjour, j'ai un problème de maths qui consiste à trouver une longueur, pour cela mon prof de maths nous a dit qu'il faut utiliser le theoreme de pythagore sauf que le triangle en question n'est pas rectangle, comment faire ?
ABC est un triangle equilateral AB=BC=AC= 14 ; D est un point intérieur à ABC:
E est un point sur la droite (AB) tel que les droites (DE) ET (AB) sont perpendiculaires, AE= 12
G est un point sur la droite (AC) tel que les droites (DG) et (AC) sont perpendiculaires, AG= 8
F est le point sur la droite (CB) tel que les droites (DF) et (CB) sont perpendiculaires
Déterminer la longueur BF.
Merci d'avance pour vos aides 
Bonjour,
écrire toutes les relations de Pythagore dans tous les triangles rectangles définis par cette figure
éliminer pour ne garder qu'une équation en x = BF
AD² = DE² + 14² = DG² + 8²
AD on s'en fiche mais ça donne une relation entre DE et DG
écrire deux autres relations du même genre
ça fait 3 relations entre DE, DF, DG et x
entre lesquelles on peut, petit miracle, éliminer (par combinaisons) DE, DF et DG et il ne reste plus qu'une équation en x
la résoudre.
PS : figure, y a qu'à demander ...
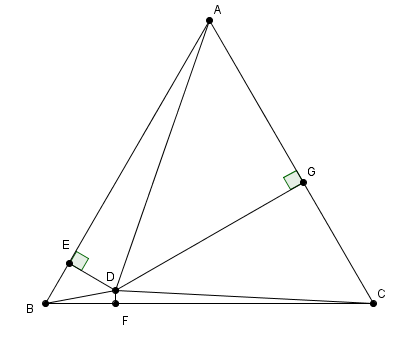
peut être faudrait-il les écrire effectivement, ces 6 relations de Pythagore (dans les 6 triangles rectangles de la figure) !!
on les combine par soustraction ...
entre lesquelles on peut, petit miracle, éliminer (par combinaisons) DE, DF et DG
bien entendu déja on élimine instantanément DA, DB et DC et il ne reste plus que 3 égalités mais sans aucun DA, DB ni DC
DA² = DE² + AE²
DA² = DG² + AG²
donne DE² + AE² = DG² + AG²
et 2 autres égalités du même genre
on en prend 2, on les retranche membre à membre et hop, une inconnue de moins
là intervient le miracle, si on combine cela avec la troisième, il ne reste aucune inconnue autre que BF = x et CF = 14-x
vu que AE, BE, AG et CG sont toutes numériquement connues
et donc l'équation en x annoncée
bon alors je vais te le faire (vu que tu n'as rien écrit ici de ce que tu as écrit sur ta feuille)
DA² = DE² + AE² = DG² + AG² (déja dit)
DC² = DF² + FC² = DG² + CG²
retrancher membre à membre ces deux égalités c'est :
(DE² + AE²) - (DF² + FC²) = (DG² + AG²) - (DG² + CG²)
(tu ne comprenais pas ce que veut dire retrancher membre à membre des égalités ?)
et tu vois bien que les DG s'éliminent !
il reste :
DE² - DF² + AE² - FC² = AG² - CG² [1]
évidemment vu que tu n'as rien écrit, toi, ici, peut être bien que ta deuxième relation était
DG² + CG² = DF² + FC² (la même chose écrite dans l'autre sens)
et que alors au lieu de retrancher membre à membre il aurait fallu ajouter membre à membre :
(DE² + AE²) + (DG² + CG²) = DG² + AG²) + (DF² + FC²)
et la aussi les DG² s'éliminent
c'est pour ça que j'ai parlé de "combiner" les égalités parce que je ne peux pas lire par dessus ton épaule les relations éxactes que tu as écrit ni sous quelle forme tu les a écrites !!
selon la forme sous laquelle tu les as écrites il faut soit ajouter soit retrancher
d'où le mot général "combiner"
la dernière relation s'écrit :
DB² = DE² + BE² = DF² + BF² qui s'écrit DE² - DF² = BF² - BE²
éliminer DE² - DF² entre cette relation et la relation [1] (combiner les deux relations) n'est plus qu'une formalité.
on a éliminé tous les trucs avec D dedans et il ne reste plus que les trucs avec A,B,C (que l'on connait) E, G (que l'on connait) et F (que l'on cherche)


