Inscription / Connexion Nouveau Sujet
quadrature du rectangle
Bonjour à tous 
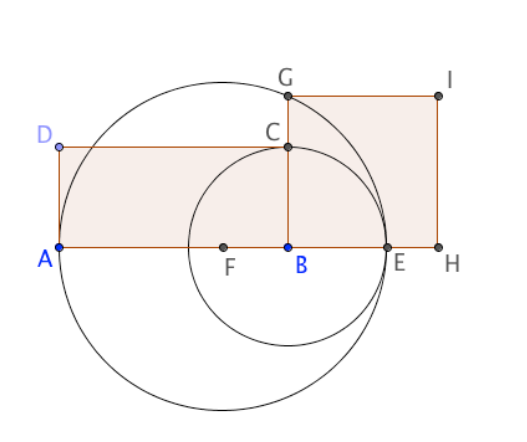
J'ai a faire démontrer la quadrature du rectangle,dont la construction est la suivante :
Construire un rectangle ABCD.
Le cercle de centre B passant par C coupe la droite
(AB) en E comme représenté sur la figure ci-contre.
F est le milieu du segment [AE].
Le cercle de centre F passant par E coupe la droite
(BC) en G.
Construire le carré de côté [BG].
Pour la démontrer je voudrais avoir 2 démos, une analytique et une autre purement géométrique..
Mais je n'y arrive pas..
Pour démo analytique, je pense qu'il faut introduire un repère, je choisi le repère orthonormé : (B,BE,BC), j'ai donc les points B(0,0), C(0,1), E(1,0) mais comment avoir les coordonnées du point A ?
Merci beaucoup pour votre aide ...
* Tom_Pascal > niveau modifié *
Bonjour,
Que faut-il démontrer niveau 3ème ?
Pour la démontrer je voudrais avoir 2 démos, une analytique et une autre purement géométrique..
Démonstration analytique niveau 3ème !
 ... Je ne sais pas faire !
... Je ne sais pas faire ! 
Bonjour,
Analytique: effectivement, ça n'a pas l'air simple d'avoir les coordonnées de A dans ton repère, peut-être peut on un choisir un mieux ? Une idée ?
Géométrique: as-tu des pistes ?
Alors la démo analytique sera pour un niveau de 2nd !
Pour la démo géométrique je ne vois pas ou démarrer...
Alors peut être prendre le repère (B,BA,BC) ? mais pour E je ne vois pas comment donner son abscisse...
repère (B,BA,BC) ca me parait prometteur oui 
Ou (A, AB, AD), au choix.
Pour la démo géométrique, je viens de le faire, et voici la méthode que je te propose:
Tu veux montrer BG^2 = AB BC
1) Tu commences par énumérer toutes les égalités vraies d'après l'énoncé. Par exemple BE = BC par construction de E.
2) Ensuite ton objectif est d'écrire BG^2 = une suite d'égalité qui te ménerait idéalement à AB BC. Donc une bonne idée serait de ramener les égalités trouvées en petit 1) en fonction de AB et BC. Puis en partant de BG^2, en utilisant les égalités de l'énoncé plus quelques égalités simples du type: AE = AF + FB + BE, tu devrais finir sur le résultat !
Petit indice: cela commence avec le théorème de Pythagore: FG^2 = FB^2 + BG^2
Bon courage !
Merci...mais je ne vois vraiment pas comment dans le repère (B,BA,BC)expremier les coordonnées de E ..
Et oui tu as raison, je ne vois pas non plus ... Peut être vaudrait-il mieux poser un repère orthonormé dont l'origine est en A (ou B si vraiment tu préfères), afin d'obtenir:
A(0,0); B(AB, 0); D(0, AD); C(AB, AD); E(AB+AD, 0)
Ceci dit, si tu n'as jamais vu ce genre de choses, c'est qu'il y a une autre solution. As tu déjà vu quelque chose de similaire ?
 Je n'avais pas vu qu'il ne s'agissait pas réellement d'un élève de troisième ! Désolé.
Je n'avais pas vu qu'il ne s'agissait pas réellement d'un élève de troisième ! Désolé.
Peut être pourrais tu poser la question dans la partie enseignement ? Je ne vois pas comment t'aider. J'y réfléchis, bon courage !
Bonjour
Géométriquement en utilisant les triangles semblables cela devrait être possible
AGE est un triangle rectangle en G ABG et GBE sont semblables
donc
L'aire du rectangle est ABBC or BC=BE
l'aire du carré est
donc on a bien l'égalité des aires
sauf erreur
salut, analytiquement avec Pythagore:
A(0,0), B(b,0), D(0,1)
1/ calculer FG et FB (tres simple)
2/ en deduire BG^2 (avec Pythagore)
BC=1 E a pour coordonnées (b+1 ,0) et Les coordonnées de F sont celles du milieu de [AE]
G est l'intersection de la droite avec le cercle de centre
et de rayon AF

 )
)
