Inscription / Connexion Nouveau Sujet
question asymptote
Bonsoir,
On a par exemple f(x) = x/2 + [ (1+lnx)/x] et C sa courbe.
On nous dit démontrer la position de C par rapport à la droite Delta d'équation y=x/2.
Montrer en particulier que Delta coupe C en un point A que l'on déterminera.
J'ai deux questions suite à cela :
1) Quand on fait f(x) - x/2 = 0 pour trouver la position C par rapport à la droite Y, doit on dériver le résultat?
C'est à dire qu'on va avoir (1+lnx)/x en résultat.
Mais pour étudier la position de C par rapport à delta, sur certains livres j'en vois qui disent qu'il faut dériver le résultat et faire un tableau de variation..
et d'autre qui avec simplement (1+lnx)/x évalue la position de la courbe.
Que faut il faire en fait alors?
et
2) Pour trouver les coordonnées du point A comment fait on?
apparemment il faut trouver A = (e-1; e-1 /2) mais je me demande comment on en arrive à trouver l'ordonnée du point A (et l'abscisse remarquez..)
Merci
bonsoir
je pose g(x) = x/2
si, sur un intervalle, on a f(x) - g(x) < 0, cela signifie que f(x) < g(x), et donc que C est située au-dessous de D
de la mm façon, si f(x) - g(x) > 0, alors C est située au-dessus de D
tu dois donc étudier le signe de (1+lnx)/x
quant au point d'intersection A, c'est simplement le point dont l'abscisse annule (1+lnx)/x
salut
pourquoi fait on f(x)-x/2 ? pour savoir si f(x)-x/2> à alors f(x)>x/2 la courbe est au dessus de l'asymptote
idem avec f(x)-x/2<0 mais la courbe est en dessous
donc en calculant la différence si tu peux faire un tableau de signe c'est gagné
2) il faut résoudre f(x)-x/2=0 et trouver x ensuite pour trouver l'abscisse il suffit de dire que ce point appartient à la droite
L'abscisse x du point A vérifie et il faut donc résoudre cette équation.
Pour étudier la position de la courbe de f et de la droite, il faut déterminer le signe de .
En général, dériver fournit des informations sur les variations. Il est parfois possible de trouver le signe à partir des variations mais le plus simple est quand-même de faire un tableau de signes. Et pour faire un tableau de signes, il convient de factoriser l'expression.
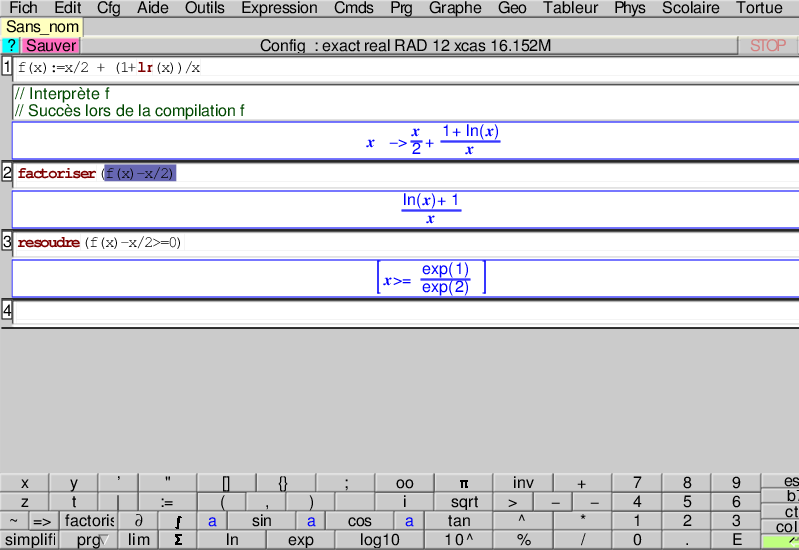
En PJ, vous trouverez des copies d'écran de XCas qui vous permettront de vérifier vos calculs. N'hésitez pas à utiliser cet excellent logiciel pour vérifier vos résultats.
A partir des calculs de XCas on sait que l'on doit prouver que la courbe est au dessus de la droite pour .
Bon courage.
P.
ou plus simplement, en remarquant que Df = R+
donc x>0
la question revient à étudier le signe de 1 +lnx ... je parie que Tesla s'en sortira s'en Xcas 
merci à vous pour vos réponses détaillées
donc dans ce cas je dérive (1+lnx)/x et je fais un tableau de signe
pour le point d'abscisse je n'ai pas compris pourquoi A = x/2 ...

je pense que tu n'as pas bien lu... inutile de dériver ici, le signe de f(x)-g(x) n'est pas difficile à trouver
quand au point A, ne te complique pas les choses :
lorsque tu étudieras le signe de f(x)-g(x), tu vas devoir résoudre l'équation f(x)-g(x)=0
et lorsque f(x)-g(x)=0, ben f(x) = g(x), non ? (les courbes s'intersectent)
et donc la solution de cette équation est l'abscisse du point A
il te suffira de calculer son ordonnée, ce que tu sais faire depuis la seconde 
de plus pour tester j'ai voulu dériver le résultat soit 1 + lnx / x
j'ai fait sous forme u'v-uv' /v2
et je trouve - lnx / x2....
bref en gros je sais pas quand on doit dériver ou faire un tableau dans ce genre de cas...
donc si y avait été égale a x-3 par exemple le point de coordonées aurait été
(e-1; e-1 - 3) c'est bien ca?
Pour la suite de l'exercice ils demandent de prouver qu'il existe un point B et un seul, de la courbe C ou la tangente T à C est parallèle à Delta.
On est pas sorti de l'auberge, je ne sais plus faire..
donc si y avait été égale a x-3 par exemple le point de coordonées aurait été
(e-1; e-1 - 3) c'est bien ca?
Bin oui si l'équation de la droite était y=x-3 ca aurait fait ca comme ordonnée
ma dérivée c'est 1/2 - lnx/x2 = 1/2
ca ferait donc
-lnx/x2 =0
j'ai dérivé ca: x/2 + [ (1+lnx)/x]
c'est bien ce qu'il fallait dériver?
Bin oui i tu cherches la tangente à la courbe c'est bien f(x) qu'il faut dériver
Et oui ta dérivée est bonne
Et donc ca fait x=?
si si mais c'était cette histoire de dérivée qui me chagrine...je ne sais pas quand on doit dériver ou non pour trouver la position de la courbe par rapport à la droite.
En tout cas merci à toi pour ton aide ( et a tout ceux qui m'ont aidé 






