Bonjour

Il n'y a pas de questions.
Joindre la courbe.

Bonjour,
Ton énoncé est incomplet
Tout le monde n'a pas le livre...

Bonjour hekla

Bonjour sanantonio312

Re-bonjour:

Désolé j'avais oublié la question : A partir de ces informations, déterminer l'expression de f .

J'ai mis ci-joint la courbe

Que proposez-vous ?

Il y a trois équations à écrire.

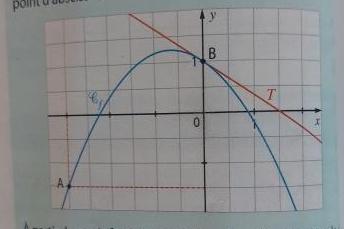
J'ai déterminé graphiquement f(-3) ;f(0) et f'(0)

f(-3) =- 1.5
f(0) =1
f'(0) = -0.7
J'avais considéré 3 points : A(-3;-1.5); B(0;1) et C(0;-0.7).
Et j'avais essayé de faire 3 équations (une pour chaque point) mais j'ai juste trouvé que c=1

Les coordonnées de C sont manifestement fausses puisque ainsi 0 aurait 2 images.

À quoi sert alors la tangente en B ?

f'(0) =-0.7x+1 ?

La tangente en B nous permet de trouver l'équation réduite y=f'a (x-a)+f(a) pour ensuite déterminer l'expression  de f ?

Non
Pas de valeur approchée, d'autre part si vous calculez la dérivée de f en 0  il ne doit pas y avoir de .

Ce n'est donc pas que vous aviez écrite, mais l'équation approximative de la tangente.

que vaut donc, ?

je sais pas

Comment lisez-vous le coefficient directeur d'une droite ?

f'(0) =1  ?

y= mx+p

m est le coef directeur (ou la pente)
p est l'ordonnée à l'origine

m=delta y /delta x

Choisissez un autre point de la tangente, vous avez déjà B
et faites le calcul de

Et par lecture graphique je pars de l'ordonnée à l'origine, je me décale de 1unité vers la droite et je descends jusqu'à la tangente (donc je descends de -0.7)

f'(0) =1/3

valeur exacte

que vaut ?

Je ne comprends pas

Je ne comprends pas pourquoi f'(0) =-2/3 alors que 1unité =2carreaux

En partant de B, vous descendez de 2 carreaux ou 1 unité et sur l'axe des abscisses vous vous déplacez de 3 carreaux ou 1 unité et demie pour atteindre la tangente.

on a donc -2/3 ou -1/1,5. Il est préférable de garder -2/3

Quelle est la fonction dérivée de définie par ?

Ah merci ! J'ai compris pourquoi f'(0)=-2/3

f'(a) =lim f(a+h)-f(a) /h ?

Si vous voulez avec , si vous n'avez pas vu les fonctions dérivées

il faut préciser

Si, j'ai vu les fonctions dérivées

alors, appliquez

Si f(x)=k alors f'(x)=0

Vous avez et pas seulement une constante

Si vous avez oublié le formulaire, vous pourrez le trouver ici Formules - Formulaire : Dérivées de fonctions usuelles

Il faut utiliser (u'*v-v'*u)/v au carré ?

Où avez-vous un quotient ?

f(x) = x au carré f'(x) =1

Que faites-vous  ?



ensuite

g(x)=bx   g'(x)=b*1
g(x)=c      g'(x)=0

Ce qui donne en regroupant le tout

f'(x)=2ax+b+0

Bien

Maintenant

f'(0)=2a*0+b+0
f'(0)=b

Bien, mais aussi on a montré que

d'où

f'(0)=-2/3 d'où  b=-2/3

Bien
On a donc à présent b et c ; manque

Il y a une donnée que vous n'avez pas encore utilisé : la courbe passe par A.

utilisée

A(-3;-1.5) appartient à Cf :
f(-3)=-1.5
a*(-3) -(2/3) +1=-1.5
a*(-3)=-1.5-1+2/3
a*(-3)=1.83
a=1.83/(-3)
a=-0.61
Donc f(x) =ax au carré +bx+c
                     =-0.61x au carré -(2/3)x+1

Erreurs de calcul

1) vous avez oublié un carré

2) il faut garder la valeur exacte 2/3

3) vous n'avez considéré que or, vous avez

g(x)=ax au carré    g'(x)=a*2x =2ax
g(x)=bx   g'(x)=b*1
g(x)=c      g'(x)=0

f'(x)=2ax+b+0

A(-3;-1.5) appartient à Cf :
f(-3)=-1.5
2a*(-3) -(2/3)*1 +1=-1.5
2a*(-3)=-1.5-1+2/3
2a*(-3)=-1.83
2a=1.83/3
a=-0.61/2
a=-0.305
Donc f(x) =ax au carré +bx+c
                     =-0.305x au carré -(2/3)x+1

Pour l'instant, on a : après remplacement de et par leur valeur

la courbe passe par A





d'où


Il me semble que vous ayez pris   ce qui ne correspond à rien