Bonsoir tout dépend du signe de f..

Bonsoir ,
Tu sais que le signe de la derivée donne le sens de variation de la fonction donc il faut connaitre le signe de f

Merci de vos réponses.
Donc si f est positif sur ]0;2[ et négatif sur ]2;5[, cela veut dire que g est positif sur ]0;2[ et négatif sur ]2;5[ comme f ou bien c'est l'inverse ??

non! ne melange pas le signe et le sens de variation de g

Ah oui c'est vrai donc si f est positif sur ]0;2[ et négatif sur ]2;5[, cela veut dire que g est  croissant sur ]0;2[ et décroissant sur ]2;5[ ? C'est ça?

oui

Mais je ne comprends plus rien du tout.😅
Dans un de mes exercices, on devais déduire les variations de g en montrant que g'= f sachant qu'on avait pas le signe de f mais ses variations , par contre on avait le signe de f'.
Mais j'étais absente ce jour là et je n'ai pas la correction.
Vous pouvez m'expliquer svp??
Merci beaucoup

Recréer un sujet avec ton exercice recopié et complet..

Très bien Merci.

Mais le soucis c'est que je l'ai déjà posté et je pensais avoir bon. Mais je n'ai pas pu avoir de correction car aujourd'hui je suis malade .😅
Le lien est ici
https://www.ilemaths.net/sujet-exercice-fonction-logarithme-728823.html#msg6333047

Bonjour,

Et qu'est-ce que tu veux qu'on écrive de plus que ce qu'on t'a déjà écrit sur cet autre topic ?

Bonjour,
En fait, tu m'as aidé sur cet exercice et je t'en remercie.
Je soucis c'est que en réalité je ne comprends pas la question où l'on doit  déduire les variations de g.
Je pensais que les variations seraient les mêmes que pour f car g'=f mais, je  ne suis pas allée en cours aujourd'hui car je suis malade. Néanmoins je pense que ma réponse est fausse mais.
Es-ce que tu pourrais m'expliquer cette question stp?

Oui je peux t'aider, masi encore faut-il que je comprenne bien ta question.

Si j'ai une fonction f ayant par exemple les variations suivante :
Croissante sur ]0;2[ et décroissante sur ]2;5[. ok
Et que j'ai une fonction g' ( la dérivée de g) qui est égale à la fonction f donc g'(x)=f(x)
Et bien quelles seraient les variations de g et bien si f(x) est négative sur un intervalle, cela veut donc dire que g'(x)<0 et donc que g est décroissante sur cet intervalle

Ah oui c'est sur😅.
Bon tu te souviens on avait trouver ( enfin plutôt vous) que g'=f.
Et maintenant je dois en déduire les variations de g.
Sauf que en déduire signifie que je dois m'aider des résultats trouvés avant. Et pour moi si je dois trouver les variations de g, j'ai besoin des variations de f. Or je ne les aient jamais calculé.
Ma question serait donc comment je déduis les variations de g?

Pardon je me suis trompé je dois avoir besoin du signe de f et je ne les aient pas du tout. Par contre j'ai le signe et de f' et les variations de f

On avait trouver ( enfin plutôt vous) que g'=f. Et maintenant je dois en déduire les variations de g.
Et bien



Tu confonds fonction négative avec fonction décroissante.
Si f=g', et bien g sera croissante si f est positive.


Quelques petits rappels qui à mon sens ne seront guère fortuits.

Pour aborder ta question (ainsi que les études qui viendront après ...), tu as à bien différencier 3 choses :
   - qu'est-ce que sont et
   - qu'est-ce que le signe d'une fonction ?
   - qu'est-ce que la variation d'une fonction ?

Autrement dit, commencer par ne pas confondre avec , ainsi que "fonction positive" avec 'fonction croissante" et "fonction négative" avec "fonction décroissante".


Donc pour commencer, c'est la fonction. Elle est définie sur un intervalle ou ensemble de départ (domaine de définition ).

Cette fonction "prend" un et le "transforme" en un qui lui appartiendra à l'ensemble d'arrivée.

Donc et

Donc et sont des réels, étant la fonction.




Pour le signe de , c'est soit , soit , ce qui correspond à la lecture sur l'axe des ordonnées.

Pour le reste, la variation de , c'est soit elle est croissante , soit elle est décroissante (soit elle est constante).

Pour ce deuxième point :
   - si est croissante, alors sa dérivée est positive :
   - si est décroissante, alors sa dérivée est négative :


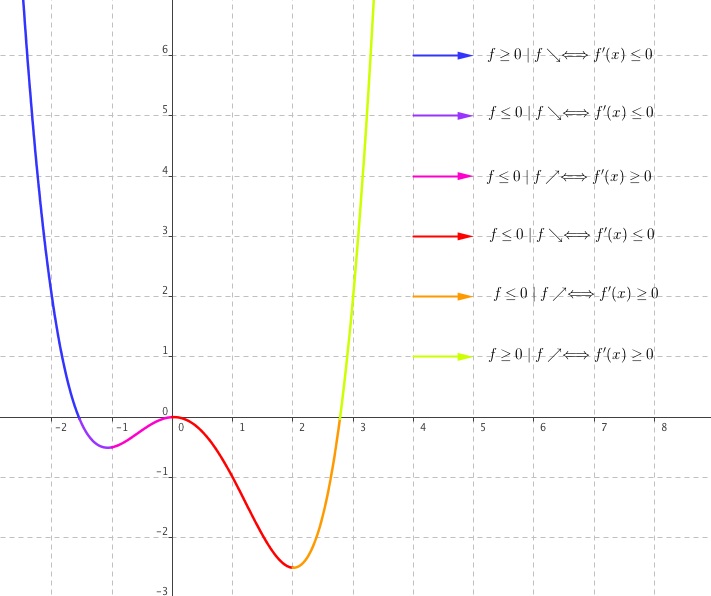
Regarde bien la courbe ci-dessous et ne considère pour l'instant que la partie en bleue.
Observe bien le fait que, si on appelle cette fonction , alors sur sa partie bleue est elle certes positive, car , mais surtout elle est décroissante, donc sa dérivée elle sera négative sur cet intervalle, soit , et donc la courbe de la fonction sera quant à elle sous l'axe des sur cet intervalle considéré.

Oh merci pour ce cours.
Mais je crois ne pas tout avoir compris.
Donc pour mon exercice j'ai ma dérivée g' qui est égale à f ce qui signifie que comme f est croissante sur ]0;2[ puis  décroissante sur ]2;5[
Et bien ma fonction g est donc croissante sur ]0;2[puis décroissante sur ]2;5[??
Désolé mais je pense avoir faux

Car je n'ai jamais, à aucun moment  montrer que f est positif ou négatif 😅 mais seulement qu'elle est croissante puis décroissante

Je ne sais pas ce que tu as montré ou pas, vu qu'on a pas ton énoncé.

Il est sur l'autre topic.
Puis-je le réécrire ici, ou je risque d'être banque?

"banque" je ne sais pas, "banni" c'est certain.

Ah oui, excuse moi c'est le correcteur 😅.
Je te mets le lien vers l'autre topic dans le cas, ou l'énoncé est écrit dans sa totalité.
https://www.ilemaths.net/sujet-exercice-fonction-logarithme-728823.html#msg6333047

Ok, vu.

Donc tu es d'accord que je n'ai pas montré que f est positif ou négatif.
Donc je ne vois pas comment on fait

Sans cette donnée je ne peux pas donner les variations de g

Répond sur ton autre topic.

..... et bien sûr que si tu les as les signes de f.