Inscription / Connexion Nouveau Sujet
Raccordement circulaire
Bonjour, aujourd'hui je me suis mis faire des annales pour préparer le concours (TS/TS') d'entrée à l'esgt, le problème c'est que je bloque sur un exercice.
Nous avons un cercle (C1) connu (centre et rayon puisque nous avons trois points), une droite (D) connus et un point P (qui n'est ni sur C1 ni sur D) connu. Nous cherchons un cercle (C2) tangent à (C1) à (D) et passant par P.
Pour ceux qui voudraient visualiser, il s'agit du second problème que vous trouverez ici :
http://www.esgt.cnam.fr/documents/concours/sujet_topo_esgt_2007.pdf
Quelqu'un pourrais t'il me donner le principe pour trouver le centre de (C2) ou un indice car je bloque complètement là.
Merci d'avance pour vos réponses
Bonjour Toufu ,
Les tangentes De P à C Coupent D en 2 points G et G' .
Je considère G (faire de même pour G'):
Le cente du cercle cherché est sur la 
de P àGP et sur la bissectrice de PG avec D .
Bonne journée .
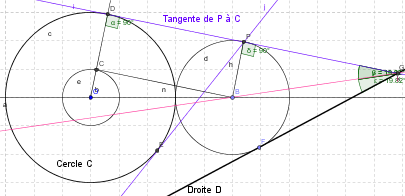
Je comprend que la bissectrice soit l'un des lieux géométriques des centres des cercles passant par P et tangent à D. Cependant, je ne comprend pas pourquoi son intersection avec la perpendiculaire de (PG) passant par P donne le centre du cercle cherché. Pourquoi les distances PB et d(B;C) sont elles égales?
J'ai également une autre question peut être idiote, mais les cercles tangents à C et à D en passant par P existent t-ils toujours?
On pourrait voir le problème sous l'angle suivant :
Le lieu du centre des cercles tangents au cercle (C1) et à la droite (D) est la parabole ayant pour foyer le point A et pour directrice une droite parallèle à la droite (D) et située à une distance de celle-ci égale au rayon du cercle (C1).
Le lieu du centre des cercles tangents à la droite (D) et passant par le point P est la parabole ayant pour foyer le point P et pour directrice la droite (D).
Le centre du cercle (C2) est donc le point d'intersection de ces deux paraboles.
Celles-ci sont bien déterminées. Reste à construire leur point d'intersection ....
Tu as compris que B (centre du cercle cherché) est sur la bissectrice .
Le cercle cherché est donc a
Tu as compris que B (centre du cercle cherché) est sur la bissectrice .
Le cercle cherché , tangent à D l'est donc aussi à GP en P .Son centre est donc sur la en P à GP .
Je comprend que le cercle de centre B est tangent à (GP) en P et à D, cependant, je ne comprend pas pourquoi il est tangent à C.
Priam, merci pour ta réponses, mais j'aurais du préciser qu'il faut pouvoir faire la construction graphiquement.
l'erreur vient du fait que le centre du cercle cherché n'a pas à être sur la bissectrice !!! excuse moi de t'avoir induit en erreur .
Je réfléchis ... et reviendrai si je trouve .
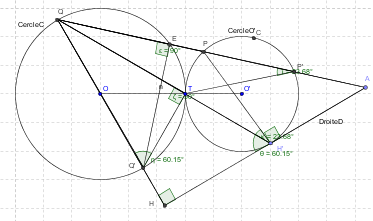
Je pense y être :
Soit H la projection de 0 sur D .
OD coupe C en Q et Q' .
QP coupe C en E ,le cercle 0' en P' et D en A .
Le cercle cherché (0') est tangent à C en T et à D en H'.
remarque Q,T et H' sont alignés .
1) Les triangles HH'Q et TQ'Q sont semblables --> HQ.Q'Q=H'Q.TQ
2) Les triangles H'PQ et P'TQ sont semblables --> H'Q.TQ=PQ.P'Q (1)
3) Les triangles EQQ' et HQA sont semblables --> HQ.QQ'=EQ.QA (2)
d'où : PQ.P'Q=EQ.QA --->PQ,EQ et QA sont connus , cela permet de construire P' .
la suite est ...
Si vous avez ,au programme ,'l'inversion , cela peut s'exprimer avec plus d'élégance :
QP.QP'=QT.QH'=QQ'.QH=QE.QA .
Donc l'inversion (Q,QQ'.QH) conserve le cercle O'
et transforme P en P' ---> d'où P' ...
Merci pour ta réponse. Oui on a vu l'inversion plane en cour mais je suis pas sur qu'on ait le droit de l'utiliser dans cet matière.
Pas mal , GaBuZoMeu ,
selon les positions relatives du cercle , de la droite et du point il y a un nombre 
de solutions ; je n'ai pas pris le temps de réfléchir à cela , mais ...quel logiciel de dessin utilises-tu ?
GeoGebra.
On peut construire les cercles solutions. Ce sont ceux passant par P et de centres les intersections de paraboles suivantes : la parabole de foyer P et directrice D (en orange) et celles de foyer 
(le centre de C1) et de directrices D' et D", parallèles à D et à une distance de D égale au rayon de C1 (en rouge).
Alors en fait en ce moment j'ai pas pu voir mon prof. On est en projet pour l'instant. Sinon, en topographie, on utilise la logique pour déterminer laquelle des solutions est la bonne solution. Ce sont des problèmes de tracé de routes. Il faut que la route parte du bon coté. Souvent dans le problème, il y a un croquis qui montre comment doit etre la forme définitive de la route.
Annuler
connectez vous
géométrie en Bts