Inscription / Connexion Nouveau Sujet
raisonnement pa réccurence et programme python
Bonjour, voici mon énoncé:
On consid`ere la suite (un) d´efinie pour tout n ∈ N par : u0 = 0 et un+1 = un + n − 1.
1. V´erifier que u1 = −1 et calculer les quatre termes suivants.
2. Montrer, par r´ecurrence, que pour tout entier n > 5 on a : un > n. En d´eduire la limite de la suite (un).
3. ´Ecrire une fonction Python permettant d´eterminer le rang n `a partir duquel un > A o`u A est
l'argument fourni par l'utilisateur.
4. Faire tourner le programme pour d´eterminer le rang n `a partir duquel un > 1000,
Pour la 1 j'ai trouvé: u1=-1
u2=-1
u3=0
u4=2
u5=5
Pour la 2, j'ai fait:
Pn :un">+n>=5
P0 est vraie car u5=5 et 5>=5>=5
Pk: uk>=k>=5
Mais je ne parviens pas à obtenir par la suite Pk+1. Pouvez-vous m'aidez s'il vous plait à trouver la démarche à réaliser.
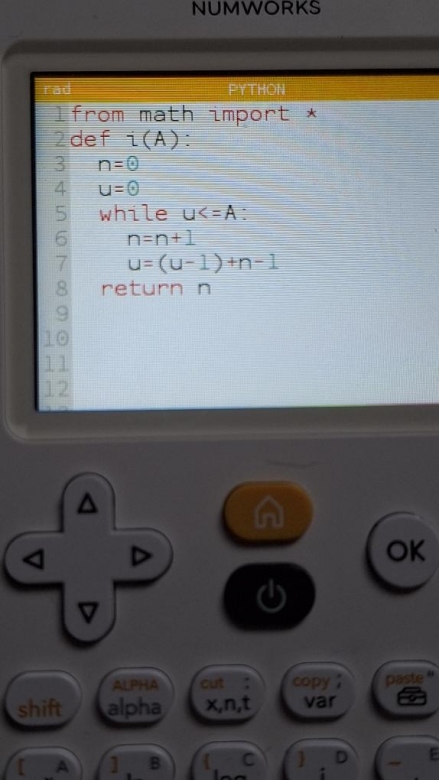
Pour ce qui est de python j'ai réalisé le programme en photo et j'ai obtenue n=47 (est ce bien cela?)
Merci beaucoup part avance à la personne qui me répondra, passez une bonne journée
Bonsoir,
votre hypothèse de récurrence est fausse.
On vous dit montrer que pour tout entier n > 5 on a : un > n.
P0 pour n=5 , u6=u5+5-1=9 >5
hypothèse de récurrence est pour Pk: uk>k
calculer uk+1
phyelec78 Merci pour ta réponse!
Comme on sait un+1=un+n-1, j'ai fait:
uk>=k d'après HR
donc uk +k>=k+k
et uk+k-1>=k+k-1
Le problème c'est que j'obtiens alors:
uk+1>=2k-1 et non uk+1>=k+1
Pouvez-vous m'aiguiller sur l'erreur que j'ai commise et comment obtenir k+1 s'il vous plait?
Passez une bonne journée!
bonjour,
en attendant le retour de phyelec78 :
tu arrives à u k+1 > 2k-1 , c'est ça ? (difficile d'y voir clair dans ce que tu écris avec les k et k+1 mal positionnés).
ne peux tu pas prouver que 2k-1 est supérieur à k+1 ?
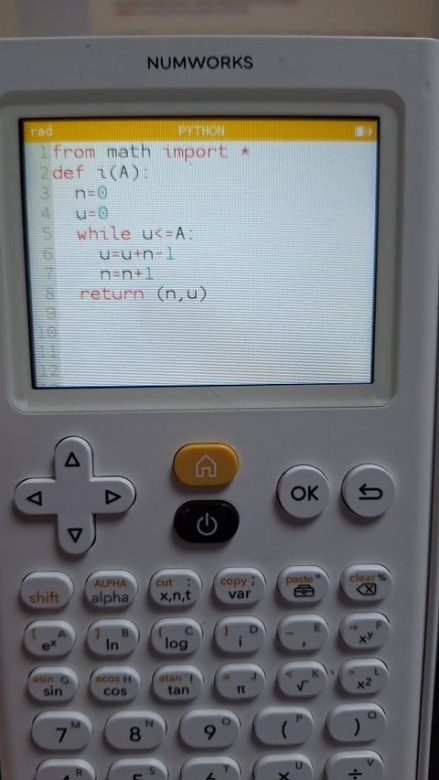
Pour le programme python, la procédure i(A) me parait bonne.
Maintenant, tu dois écrire le "corps" du programme (3 lignes) qui demande une valeur pour A et qui affiche la valeur de n correspondante.

 .
.

