Bonjour
les côtés homologues ne sont pas justement AB et AD ?

As-tu utilisé quelquepart le fait que la droite (AN) est la bissectrice de l'angle BAD ? Il faudrait bien utiliser cette information...
Que peux-tu dire du triangle ABN ?

Bonjour !
Que viennent faire ici DC et DM qui ne sont pas des côtés de tes triangles ?

Il y a déjà eu une réponse pour trouver le rapport que tu souhaites.

Bonne continuation.

PS ? Ta question concernant les côtés à prendre : il faut faire les rapports des côtés opposés aux angles que tu as repérés comme égaux (tu en as déjà deux qui conviennent). Au cas où tu l'aurais oublié, si tu as déjà deux angles égaux, les troisièmes angles restants le sont aussi.

Robot, ça a été utilisé pour dire que les angles en A des deux triangles sont égaux

Leelao, le rapport AB/AD est donné dans l'énoncé ....

lafol, je ne pense pas sûr que Leelao l'ait utilisé pour montrer que les triangles sont semblables :

        

marrant, pour moi les angles égaux étaient en A, et en D/B... comme quoi ...

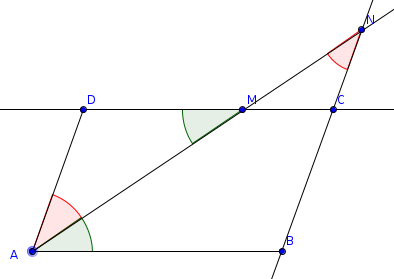
Penser aux angles alternes_internes quand on a une droite qui coupe les côtés d'un parallélogramme me semble assez naturel.

maintenant que tu le dis, oui, moi je m'en servais après coup pour montrer que des tas de triangles de la figure sont isocèles
comme leelao n'a pas dit quels étaient les deux angles égaux, en effet, on ne sait pas quelle a été sa démarche à elle (ou lui ?)