Inscription / Connexion Nouveau Sujet
rectangle d'or
Bonjour
Si quelqu'un pouvait m'aider pour résoudre un ex SVP Merci
On a un rectangle de longueur L et de largeur l (L > l).On dit que ce rectangle est un rectangle d'Or lorsque le rectangle obtenu en ôtant le carré de côté l au rectangle initial lui est semblable.
1- Relation caractéristique du nombre d'or
Montrer qu'un rectangle est un rectangle d'or lorsque L et l vérifient:
L/l= 1/L-l
2- a = nombre d'or
on pose a=L/l
Montrer que: a>o et a²=a+1
SVP
Bonjour,
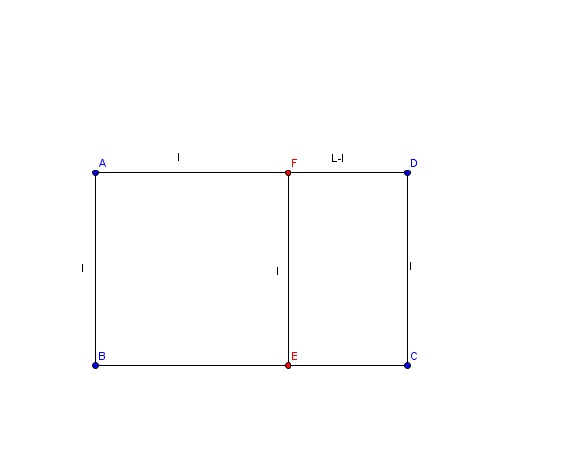
Pour que soit en "or", il faut que les rectangles
et
soient semblables, c 'est à dire:
ou bien:
ou bien encore:
puis en divisant les deux membres par :
et en posant
:
soit
Bonjour,
tout d'abord ton énoncé est faux, car pour le 1) il faut montrer en fait que L/l= l/(L-l).
1) Les deux rectangles étant semblables, ses côtés correspondants sont dans un même rapport de proportionnalité. Donc "grande longueur"/"petite longueur" = "grande largeur"/"petite largeur", ce qui donne avec les mesures: L/l = l/(L-l).
2) a = L/l.
Du 1) on a: L/l = l/(L-l) = 1/(L/l - 1) donc a = 1/(a-1) et comme a>0, on obtient: a(a-1) = 1, soit: a² = a+1.
Voilà,
padawan.
Annuler
connectez vous