Inscription / Connexion Nouveau Sujet
rectangle et triangle isocèle
Dans le camp de base d'une expédition de géologue , le matériel électronique est rangé dans une caisse ( parallélépipède rectangle de dimension h x l x L). Pour protéger la caisse on la dispose sous un abri en toile de type"tente canadienne" de 2 mètres de long et dont la section droite perpendiculaire aux deux pans du toit est un triangle équilatéral de un mètre de coté . la caisse fait la même longueur que la tente et toutes ses arrêtes sont en contact , soit avec le tapis de sol soit avec la tente ( sans la déformé ). la caisse occupe exactement la moitié du volume de la tente .
quelles sont les dimension de la caisse ??
voici mes recherches
on sait donc que l=2
j'ai réussi a démontrer que L=1-2x
redimensionne ton image avec paint ou autre logiciel de traitement d'images, choisis une extension où tu peux réduire la qualité
voila ce que j'ai réussi a faire mais je ne sais pas comment trouver les dimensions de la Largeur ??
merci de votre compréhension
bonne journée 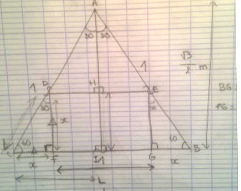
***image tournée et retravaillée pour la rendre lisible ! ***
suite 3 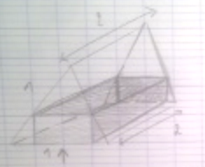
***image recadrée sur la figure***et retravaillée pour la rendre lisible***tu as lu le mode d'emploi du site ?....seules les figures sont admises, tu dois recopier tes calculs et tes raisonnements***bon pour une fois car je vois que tu es nouveau(velle)
Je ne sais pas quelle calcul faire pour trouver ces longueurs , j'ai reussi a trouver que la hauteur du triangle est de environ 0,46 que chasur triangle est rectangles ,
Je ne sais pas quelle calcul faire pour trouver ces longueurs , j'ai reussi a trouver que la hauteur du triangle est de environ 0,46 que chaque triangles est rectangles ,
Bonjour,
il faut bien comprendre que en coupe la tente est un triangle équilatéral de 1 m de côté et la caisse un rectangle dont les deux dimensions largeur et hauteur sont inconnues
la longueur commune L = 2m de la tente et de la caisse n'intervient absolument pas dans le problème pour l'instant puisqu'elles sont les mêmes et donc le problème revient à inscrire un rectangle dans un triangle équilatéral de telle sorte que le rectangle ait une aire moitié de l'aire du triangle
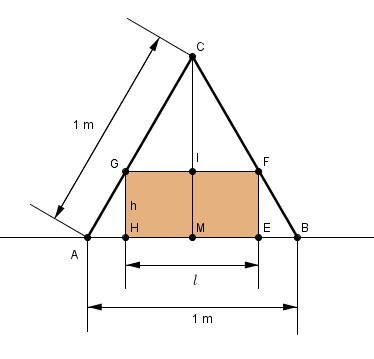
calculer en fonction de
(avec Thalès, en utilisant
et la hauteur MC, à calculer, pas "environ 0,46", d'ailleurs faux, mais sa valeur exacte avec racine carrée écrite racine carrée et pas de calculette du tout)
écrire alors l'aire du rectangle en fonction de (que de
)
écrire que cette aire est la moitié de celle du triangle (la calculer, pareil, en valeur exacte et pas à la calculette)
ça donne une équation en la seule et unique inconnue , résoudre
terminer l'exo en calculant h.
merci mathafou pour votre réponse mais je ne voie pas comment calculer h en fonction de l , j'arrive a trouver que la hauteur = (racine de 3 ) x /0,5
Bonjour
je n'ai pas la réponse mais comment as tu trouvé la hauteur de la tente?
tan30=
 0,87; non?
0,87; non?j'ai utilisé Pythagore pour la hauteur je trouve--> racine de 3 / 2
bien égale a environ 0,87
l'aide de mathafou te sera bien utile 
tu prendras donc comme il le précise la valeur exacte de tan30 soit
la hauteur de la tente est bien
ça c'est CM sur mon dessin
maintenant il faut écrire Thalès pour exprimer la hauteur de la caisse en fonction de
au choix, dans ACM et AGH
ou dans CAM et CGI
les deux aboutissent.
autre méthode avec la trigo :
etc
AH s'exprime facilement (simple soustraction) en fonction de
dans les deux cas on a bien (de la caisse) en fonction de l (de la caisse) etc
Oui mais on travaille dans le triangle ACM pour calculer CM donc on le déduit bien de tan(30)
Oui merci d'avoir corrigé Glapion
dans ACM on a aussi bien
CM = AM/tan(30°)
que CM = AM×tan(60°)
ça c'est pour calculer CM
je parlais du calcul de h = GH, hauteur du rectangle
pour lequel on a exactement pareil
aussi bien
GH = AH/tan(30°) que GH = AH×tan(60°), comme on veut (donnant bien entendu le même résultat vu que tan(60°) = 1/tan(30°)
et de toute façon aussi bien l'un que l'autre peut se traiter sans trigo du tout avec Pythagore pour CM et avec Thalès pour GH


 3/3 et pas /2
3/3 et pas /2
