Inscription / Connexion Nouveau Sujet
Rectangle inscrit dans un triangle
Bonjour a vous j'aurai besoin de votre aide:
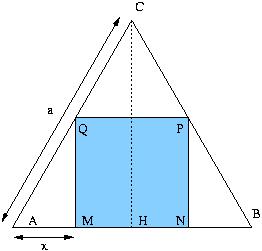
Soit un triangle équilatéral ABC de côté a. On inscrit dans ce triangle un rectangle MNPQ. On pose x=AM.
Pour quelle valeur de x l'aire du rectangle est-elle maximale?
VOila en esperant que vous pourrez m'aider.
Voilà, je pense que mon dessin va t'aider. Il faut remarquer que les triangles AHC et AMQ sont semblables.
Comme le triangle ABC est équilatéral de côté a, la hauteur du triangle vaut .
Donc la hauteur du rectangle est .
L'aire du rectangle vaut A(x)=.
À toi de jouer.
 Isis
Isis
donc il suffit d'etudié A(x) de trouvé son maximum?? mais pour trouver son maximum il faut etudié la derivé ?? si oui sur quelle intervalle stp?
Les bornes de x viennet de la nature géométrique du problème. On peut prendre x=0 jusqu'à x=a/2.
Il faut effectivement dériver la fonction et étudier les variations pour être sûrs d'avoir un maximum.
Isis
a ok mais je ne comprends pas comment etudié A(x) car ya x et a enfin tu peux m'aider stp?
Ne te laisse pas encombrer par le a, fais semblant de le connaître. Tu peux traiter le a comme tu aurais traité un 2 ou  .
.
Peut-être qu'en faisant d'abord la distributive tu arrives mieux à dériver:
Si tu n'arrives pas à faire cet exercice, écris ici au moins ce que tu as pu faire et je pourrai mieux t'expliquer les points qui te posent problème.
Isis
ok ba deja j'ai unn probleme c'est que j'arrive aps a derivé cette fonction :s donc ca demarre malet en plus cette exercice doit etre fni avant ce soir donc voila :s:s
Ce n'est pas pour ça que je vais le faire pour toi. L'important à mon avis est de comprendre et non pas de montrer un beau devoir au prof.
Tu connais la règle pour dériver les polynômes ? Ou tu dois passer par les limites? Tu sais que
? Si tu sais tout ça il suffit de l'appliquer. Si tu n'es pas au clair avec au moins une de ces règles tu peux demander, je suis encore là un moment.
Isis
Isis
nan je connais les derivées des polynomes c bon mais le porbleme c'est que la j'arivve aps a derivé la racine du polynome c poir ca
Mais tu n'as pas de racine à dériver. Je pense que tu sais que si c est une constante. Maintenant si
ça ne change rien. On a
.
Isis
donc la derivé c'est 1/2racine3x-1/4x ????
Je ne vois pas d'où tu sors tes fractions.
Peut-être que tu confonds ces deux lignes
Une fois le x est sous la racine et l'autre fois il n'est pas sous la racine.
Isis
HAAAAAAAAA d'acord je comprends mieu maintenant
donc il suffit mainteant de ressoudre f'(x)=0 et apre d'etudié les variaion de f(x) et den ddeudire le maximum?
g le même problème que ljames.
pouri vou méé pr ésoudre f'(x)=0
voici mon résulta:
a 3= 4
3= 4 3 x
3 x
x=(a 3)/(4
3)/(4 3)
3)
x=a/4.
aprè je ne c pa komen fèr...aidé moi plizzzz


