Inscription / Connexion Nouveau Sujet
Représentation graphique d'une fonction
Bonsoir,
J'ai une question d'un exercice dont je ne suis pas sûre de ma réponse. Est-ce que vous pourriez m'aider ? Merci.
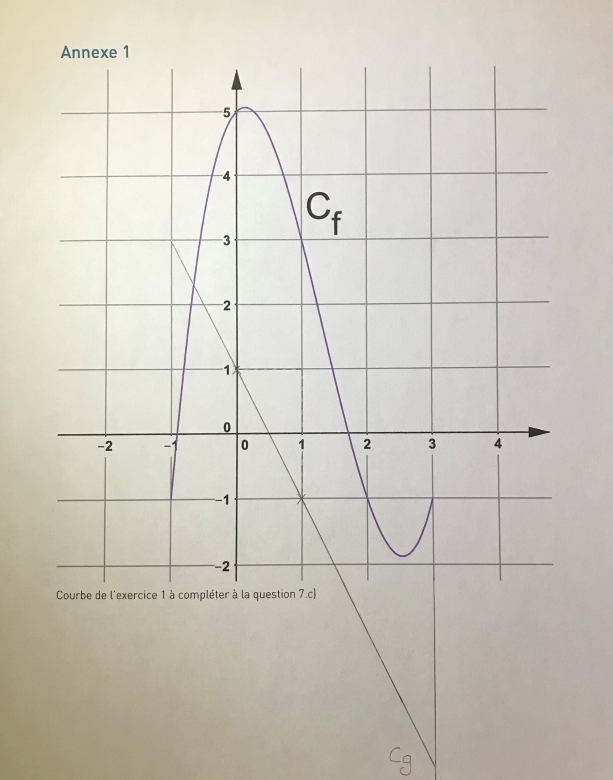
- On considère la fonction f et g définie sur [-1 ; 3] par g(x) = -2x+1. Comparer les deux fonctions f et g.
Ma réponse est :
La fonction f est une fonction polynôme de degré 3 sur l'intervalle [-1 ; 3] alors que la fonction g est une fonction affine, droite décroissante également sur l'intervalle [-1 ; 3].
Bonsoir
Souvent comparer deux fonctions c'est dire la position relative d'une courbe par rapport à l'autre
Bonsoir,
Ce peut être aussi dire comparer f(x) et g(x), autrement dit étudier le signe de f(x)-g(x). 
Merci pour vos réponses.
Ce n'est pas la seule question de l'exercice, dans les questions précédentes on me demandait de :
- donner les images, les antécédents et les extremums
- résoudre des équations et inéquations
- dresser le tableau de variation de la fonction f ainsi que le tableau de signes
- donner la nature de la fonction g ainsi que de la courbe représentative Cg
- puis de tracer la courbe de la fonction g (que j'ai faite)
J'ai réussi à répondre à toutes ces questions.
Maintenant, je bloque un peu et dans l'énoncé il ne me donne pas l'expression de f(x).
Est-ce qu'il faut que je compare ces deux courbes en étudiant le tableau signes de f(x) et g(x) ?
Merci
la FAQ du forum
bon, cela n'engage que moi, mais vu le problème, je dirais que cette dernière question est un peu "débile"...
comparer, pour nous, oui, c'est dire qui est plus grand, qui est plus petit
donc il va falloir te fier au dessin, mais tu ne connais pas la valeur exacte de l'abscisse du point d'intersection entre les deux courbes
tu l'appelle alpha par exemple en disant par lecture graphique 
....
ensuite pour
x 
]-
, [....etc
...vois-tu ?
pour x ]- ; [, compare f(x) et g(x)
puis f()=g() puisque c'est l'abscisse du point d'intersection
puis pour x ], + [, compare à nouveau f(x) et g(x)
ce sont les x qui sont dans le même intervalle, et les x se lisent sur l'axe des abscisses
je te demande de comparer f(x) et g(x), les images, et elles, elles se lisent sur l'axe des ordonnées
La fonction g(x) est d'ordonnée 3 et f(x) est d'ordonnée 5,1 donc la fonction f(x) est plus grande que la fonction g(x).
bof bof bof
lis cette fiche, tu y verras peut-être plus clair
Etude de la position relative de deux courbes
Bonjour,
Pour x ]-1 ; -0,9[U]1,7 ; 3[ alors f(x) < 0 donc f(x) < g(x) donc la courbe Cf est en dessous de la courbe Cg.
Pour x ]-0,9 ; 1,7[ alors f(x) > 0 donc f(x) > g(x) donc la courbe Cf est au-dessus de la courbe Cg.
Est-ce bon ?
oui, TB (tu remplaceras ton -07 par qui vaut environ -07), mais c'est ça qu'on te demande
et donc 2e question :sur l'intervalle ] ; 3] quelle est la courbe au dessus de l'autre et donc qui est le plus grand entre f(x) et g(x)
Du coup pour répondre à la question de l'exercice qui est de comparer les deux fonctions f et g, je note :
Sur l'intervalle ]-1 ; [, g(x) est plus grand que f(x).
Et sur l'intervalle ] ; 3[, f(x) est plus grand que g(x).
J'ai juste une dernière question, pourquoi l'appelle-t-on alors que je peux trouver son abscisse et son ordonnée en lisant sur le graphique ?
Merci
correct
la lecture graphique ne donne qu'une valeur approchee de alpha
remplacer alpha par -0.7 n'est correct que si alpha vaut exactement -0.7 ce qu'on ignore ici
Dans cet exercice on regarde le graphique pour en deduire une comparaison de f(x) et g(x)
Mais souvent on demande d'etudier la position relative des 2 courbes. Dans ce cas il faut etudier le signe de f(x)-g(x) ou de g(x)-f(x) pour en deduire la position relative des 2 courbes
Annuler
connectez vous