Inscription / Connexion Nouveau Sujet
Représentation graphique des termes d'une suite.
Bonsoir ,
Merci d'avance. 
Soit la suite (un) définie par :
1) Représenter les 4 premiers termes A0 , A1 , A2 et A3 de cette suite.
2) Justifier que les abscisses respectives des points A1 , A2 ,A3 sont u1 ,u2 ,u3.
Réponses
1)
Soit (C) la représentation graphique de la fonction dans le plan muni du repère orthonormé (O ; I ;J) et (D) la droite (D) la droite y = x.
A0 est le point de (C) d'abscisse u0.
Je construis A1 en projetant sur (D) parallèlement à (OI) ; le point obtenu est ensuite projeté sur (C) parallèlement à (OJ).
De la même façon, je construis A2 à partir de A1 , puis A3 à partir de A2.
Voilà ce que j'ai :
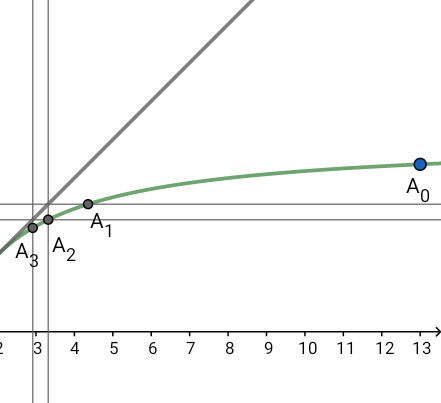
2) Je n'y arrive pas.
Le but de l'exo est de pouvoir construire les points A1 , A2 et A3 à partir de A0 d'abscisse u0..
Alors ces points sont définis par leurs abscisses u?
Mais faut que je le démontre par calcul..
Bonsoir,
mets donc des pointillés, histoire qu'on y voie quelque chose. Nommes les coordonnées des points. Et pas besoin de calcul , la courbe de f suffit.
2) Justifier que les abscisses respectives des points A1 , A2 ,A3 sont u1 ,u2 ,u3.
.
Le but de l'exo est de pouvoir construire les points A1 , A2 et A3 à partir de A0 d'abscisse u0..
Alors ces points sont définis par leurs abscisses u?
clairement il y a contradiction entre les deux versions. Un énoncé complet et exact, et pas ce que tu penses en avoir compris, est nécessaire pour te donner des réponses satisfaisantes
Bonjour, oui je vois que que tu connais le procédé graphique pour visualiser les valeurs d'une suite récurrente.
tu as la méthode expliquée là si tu veux ![]()
tu dessines la courbe et la droite y=x qui sert à rabattre les points de l'axe des y sur l'axe des x pour pouvoir continuer la récurrence. Les segments semblent rebondir un coup sur la courbe et un coup sur la droite; A chaque verticale bleue, il y a un terme de la suite.
Si tu connais bien le procédé, la réponse à la question 2 est plutôt facile.




