Inscription / Connexion Nouveau Sujet
résolution inéquation
bonjour a tous. Voila il s'agit d'une inéquation toute bete mais que je n'arrive pas a résoudre.
1) Dévelloper l'expresssion (x-1/2)^2 -1
2) En déduire une factorisation de x^2-3/4
3) Résoudre l'inéquation x^2-x-3/4 < 0
Voila je tiens a préciser que les deux premieres j'ai réussi a les faire mais il s'agit du 3) du fait que je sais ou placer et comment isoler le x.donc si vous pouviez m'aider?
J'ai mis les deux premiers questions parceque ca fait parti du meme exercice et que c'est censé aider pour le troisieme.Merci d'avance
Bonjour,
puisque tu as factorisé (x²-x-3/4), sers toi du résultat pour résoudre l'inéquation
x² - x - 3/4 < 0
à l'aide d'un tableau de signes par exemple...
SLT voila je suis tombé sur une question que je ne comprend pas vraimen.
Résoudre graphiquement l'inéquation x²-x-3/4<0(justifier en rédigeant).
Voila comment fait on cela?
*** message déplacé ***
Bonjour.
Trace la fonction x ---> x² - x - 3/4.
L'ensemble des solutions cherché est l'ensemble des réels pour lesquels le graphique est "sous" l'axe des abscisses.
*** message déplacé ***
Bonjour,
Tu fais un tableau de valeurs pour tracer la courbe représentative de f(x)=x²-x-3/4, et tu regarde sur quel(s) intervalle(s) les points de cette courbe ont une ordonnée négative.
Pour la justification, tu as déjà fait cet exercice il y a une semaine : 
résolution inéquation, c'est la suite ?
*** message déplacé ***
Bonjour,
Le 3) est une inéquation du second degré, on doit donc calculer le discriminant est voir s'il est positif, négatif, ou égal à zéro.
Si on le fait, on trouve que 
=(-1)²-4*(-3/4)=1-(-3)=4
Le discriminant est donc positif.
Cela nous indique donc le nombre de solutions, qui est égal à 2 lorsque ce dernier est positif.
Les deux solutions sont :
x'=(-b-
)/2a
x'=(-(-1)-4)/2
x'=(1-2)/2=-1/2(=-0,5)
x"=(-b+)/2a
x"=(-(-1)+4)/2
x"=(1+2)/2=3/2(=0,5)
Lorsque le discriminant est positif, ce qui est le cas, on peut factoriser sous la forme a(x-x')(x-x")
[x-(-1/2)][x-3/2]
0
(x+1/2)(x-3/2)0
On étudie ensuite le signe de x+1/2 :
x+1/2>0
x>-1/2
On étudie ensuite le signe de x-3/2 :
x-3/2>0
x>3/2
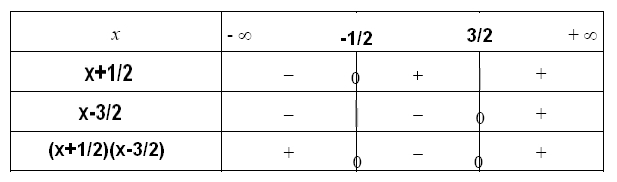
On sait également que dans un tel trinôme du second degré, là où le discriminant est positif, ce dernier est du signe de -a entre les racines (calculer juste au-dessus (-1/2) et (3/2)) et du signe de a à l'extérieur des racines, dans un tableau de signe. Que tu peux voir ci-dessous, je te l'ai attaché à ce topic.
D'où la solution de l'inéquation : -1/2x3/2, c'est à dire S={-1/2;3/2}
Annuler
connectez vous