Inscription / Connexion Nouveau Sujet
résolutions d'équations et d'inéquations
Bonsoir, je suis bloquée dans la résolution de l'exercice, et j'ai vraiment besoin de votre aide pour le résoudre
ENONCE
f(x)=x/(x-1)(x-4)
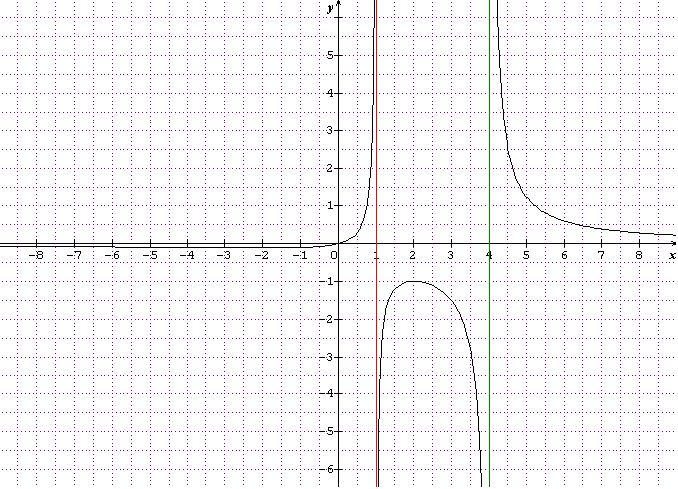
1)Etuduez la fonction f et tracez sa courbe représentative dans un repère choisi.
2)Discutez graphiquement selon les valeurs de m le nombre de solutions de l'équation f(x)=m
REPONSES
1)J'ai fais l'étude de la fonction mais je doute que c'est correct
Df:]- ,1[
,1[ ]1,4[
]1,4[ ]4,+
]4,+ [
[
limf(x)=x/x2=1/x=0
x -
-
limf(x)=x/x2=1/x=0
x +
+
lim x= 1
x 1 Par quotient lim f(x)=-
1 Par quotient lim f(x)=-
lim(x-1)(x-4)=0- x 1-
1-
x 1
1
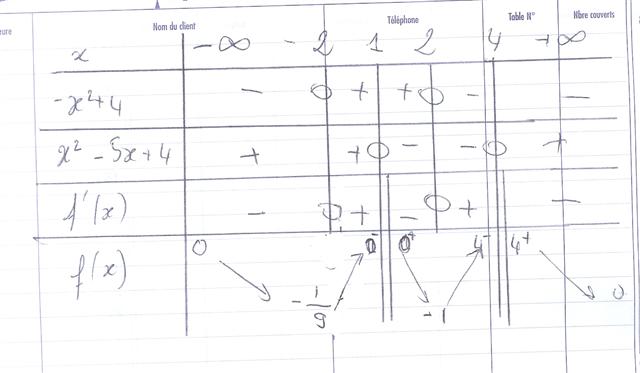
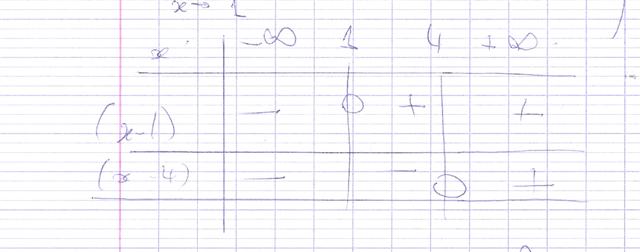
je ne sais pas faire des tableaux de valeurs, alors je l'ai scanné
lim x=1 Par quotient limf(x)=+
x 1 x
1 x 1+
1+
lim(x-1)(x-4)=0+
x 1+
1+
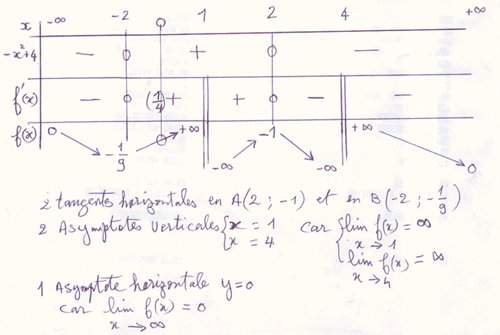
Asymptote verticale d'équation x=1
lim x=4 Par quotient lim f(x)=-
x 4 x
4 x 4-
4-
lim(x-1)(x-4)=0-
x 4-
4-
lim x=4 Par quotient lim f(x)=-
x 4 x
4 x 4+
4+
lim(x-1)(x-4)=0+
x 4+
4+
Asymptote verticale d'équation x=4
maintenant je calcule la dérivée :
f(x)=x/(x-1)(x-4)
u(x)=x v(x)=x2-5x+4
u'(x)=1 v'(x)=2x-5
f'(x)=(x2-5x+4-x(2x-5))/(x2-5x+4)2
=(x2-5x+4-2x2+5x/(x2-5x+4)2
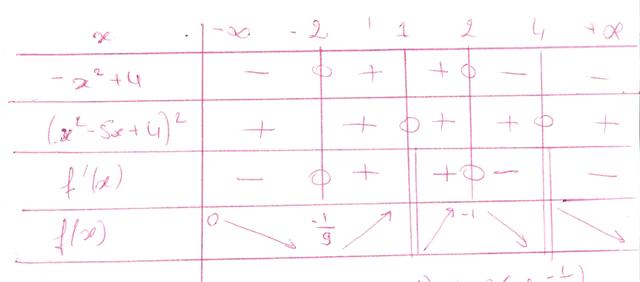
=(-x2+4)/(x2-5x+4)2
Ici je suis sûre que j'ai fais une erreur donc je n'ai pas continué.
voilà ce que j'ai pû faire, et j'ai sùrement fais des erreurs.
J'ai donc besoin de votre aide 
Cordialement

Je vous remercie énormément!!
merci mille fois 
mais un problème persiste, je ne comprends pas la question , je ne comprend pas le f(x)=m ??
Cordialement

aussi, j'ai vérifié mes calculs sur les limites, j'ai retrouvé les erreurs quand x tend vers - et quand x tend vers +
et quand x tend vers + mais je n'ai pas compris pourquoi j'ai fais un erreur là où vers tend vers 4.
mais je n'ai pas compris pourquoi j'ai fais un erreur là où vers tend vers 4.
ça me donne lim f(x)=-
x 4-
4-
et lim f(x)=+
x 4+
4+
j'avance ces réponses grâce au tableau, et j'ai le même tableau après correction
Cordialement


 =16
=16