Inscription / Connexion Nouveau Sujet
Seconde quadrilatère IJKL
Bonjour, j'aurais besoins d'aide pour la question 1 est la question 3 s'l vous plait.
En utilisant les nouvelles formules et en se plaçant dans le repère (A,B,D) ; refaire l'exercice :
Exercice: Soit ABCD un quadrilatère. Soit I le milieu de [AB]. Soit J le milieu de [BC]. Soit K le milieu de [CD]. Soit L le milieu de [DA].
1. Montrer que IJKL est un parallélogramme.
2. Quelle condition nécessaire et suffisante donner (sur les diagonales du quadrilatère ABCD) pour que
a. le quadrilatère IJKL soit un rectangle ?
b. le quadrilatère IJKL soit un losange ?
c. le quadrilatère IJKL soit un carré ?
3. Soit IJKL un parallélogramme (non aplati). Soit A un point du plan. Soit B tel que I soit milieu de [AB]. Soit C tel que J soit milieu de [BC]. Soit D tel que K soit milieu de [CD]. Soit A' tel que L soit milieu de [DA']. Montrer que A' = A
Merci beaucoup d'avance j'en serais très reconnaissante
Bonjour
Que proposez-vous ?
Qu'est-ce qui vous gêne ?
Avez-vous réalisé une figure ? Vous pouvez la joindre.
Bonjour, alors pour la 1 j'ai réussi à faire quelque chose mais la 3 non.
Pour la 1 j'ai mis : IJKL est un parallélogramme car les côtés opposés sont deux à deux parallèles. Par applications du théorème des milieux, on montre que les côtés opposés de IJKL sont chacun parallèles à une diagonale de ABCD, donc parallèle entre eux.
ce qui me gêne c'est que je suis vraiment nulle en maths et je comprends pas du tout la question 3 et non je n'est pas de figurer et je ne l'ai pas faite car tout simplement je n'y arrive pas.
Par l'absurde
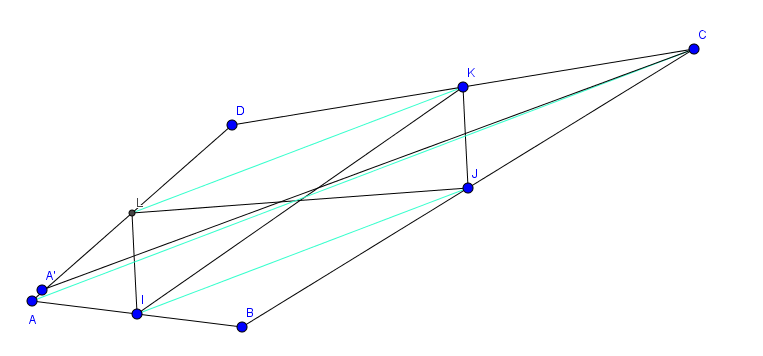
la figure est manifestement fausse.
Que pouvez-vous dire de (IJ) et de (AC) ?
De (CA') et de (KL) ?
De (IJ) et (KL) ?
Que pouvez-vous dire de C ?
Bonsoir,
si je peux me permettre, vous me direz .....
Les vecteurs sont encore au programme de seconde j'ai l'impression. Ce serait peut-être plus simple à utiliser ?
Si je ne me trompe pas IJ et AC sont paralleles que CA' et KL le sont aussi. je n'y arrive pas et je suis super fatiguée pouvez vous m'aider svp
Oui on a (CA') et (CA) qui sont toutes deux parallèles à (IJ) ou (DK)
Or par un point pris hors d'une droite, on ne peut mener qu'une parallèle à cette droite. On pourrait mener par C deux parallèles à (IJ) donc les droites sont confondues
Ce que vous venez d'écrire
les droites (AC) et(IJ) sont parallèles (droite des milieux).
les droites (A'C) et(KL) sont parallèles (droite des milieux).
Or (IJ) et (KL) sont parallèles IJKL étant un
On a donc passant par C deux droites parallèles à (KL). Cela ne se puit.
Par un point pris hors d'une droite, on ne peut mener qu'une parallèle à cette droite donc (CA)=(CA') et par suite A=A'
Vous pouvez proposer votre solution avec les vecteurs.
J'en étais resté au cinquième postulat d'Euclide.
J'avais plutôt idée de laisser lolantd chercher un peu, tout en donnant des pistes.
Mais les points de vue sont tout de même différents et je crains qu'il soit un peu perdu.
On voit cela plus tard ?
Je vous le dit sincérement ca fait 5h je suis dessus j'en peux plus juste dit moi si vous voulez bien m'aider c'est tout sinon j'abandonne
Dans le raisonnement précédent, il faut aussi considérer la longueur
On avait l'alignement des points, mais c'était insuffisant pour l'égalité
Vous savez quoi laisser tomber, ca fait 2h je demande l'aide je vous dit de ma proposer votre idée vous ne le fait pas et bin laisser tomber ce n'est pas grave je vais arreter de me prendre la tête
Ici on donne des explications, des pistes mais pas de réponse toute faite.
Tu dis être crevé donc arrête là.
En utilisant la droite des milieux et le postulat d'Euclide, on a montré que les droites (CA) et (CA') étaient confondues.
Pour affirmer que les points A et A' étaient les mêmes, il faut utiliser l'autre particularité de la droite des milieux.
Le segment a pour longueur la moitié du troisième côté
donc on a CA'=2KL d'une part CA=2IJ d'autre part
Comme IJ= KL on a donc CA=CA' les points A et A' sont donc confondus
Laissez tomber hekla, cette personne est irrespectueuse, et si je lis bien, attend une réponse toute faite à recopier "pour demain"
Il était possible de poser cette question avant aujourd'hui j'imagine, auquel cas nous aurions tous pu prendre un peu plus de temps



