Inscription / Connexion Nouveau Sujet
Sections planes d'un cylindre
Bonjour à tous,
J'ai un exo de spé mais je comprend vraiment pas (on vient juste de commencer le chap)
Enoncé:
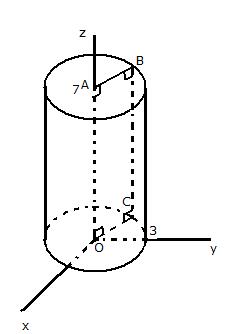
La figure ci-dessous représente le cylindre de révolution engendré par la rotation du segment [BC] autour de l'axe (Oz), le quadrilatère OABC étant un rectangle. Le point A a pour coordonnées (0, 0,7) dans le repère orthonormal (I, ,
, ,
, ) et AB = 3. Analytiquement, le cylindre est l'ensemble des points M de l'espace dont les coordonnées (x,y, z) vérifient :
) et AB = 3. Analytiquement, le cylindre est l'ensemble des points M de l'espace dont les coordonnées (x,y, z) vérifient :
x² + y² = 9 et 0  z
z  7
7
Nous nous intéressons maintenant à l'ensemble S des points M (x,y,z) de l'espace, dont les dont les coordonnées (x,y, z) vérifient :x² + y² = 9
1. Prouvez que tout point M de S est à la distance 3 de l'axe (Oz) et réciproquement, que tout point situé à la distance 3 de l'axe (Oz) est un point de S.
2. On rappelle que le plan P d'équation z = 5 est parallèle au plan (xOy) (d'équation z=0). P est l'ensemble des points M(x,y,z) de l'espace tel que z = 5.
a) Expliquer pourquoi l'intersection de ce plan P et du cylindre S est un cercle centré sur l'axe (Oz) de rayon 3.
Je dirais que le plan P étant parallèle à (xOy), il coupe S, et donc l'intersection d'un plan et d'une sphère étant un cercle, et comme S a un rayon de 3, l'intersection de P et de S est un cercle centré sur l'axe (Oz) de rayon 3.
b) Quelle est l'intersection de S avec le plan d'équation z=-4 ?
Je pense qu'il y en a pas car z  [0, 7].
[0, 7].
3. M () est un point de S et un
 réel quelconque
réel quelconque
a) Que pouvez vous déduire du point N de coordonnées ( +
 ) ?
) ?
b) Déduisez-en qu'il existe des droites contenus dans la surface S.
4.
a)Quelle est l'intersection de la surface S avec le plan d'équation x=0 ?
b) Quelle est l'intersection de la surface S avec le plan d'équation y=0 ?
c) Quelle est l'intersection de la surface S avec le plan d'équation x=1 ?
d) Plus généralement, quelle est l'intersection du cylindre d'équation x² + y² = r² avec le plan d'équation x =a ? Avec le plan y = b ? Que se passe t il pour a = r ? pour b=r
Surface de S et S c'est pareil?
Merci beaucoup de m'aider à comprendre cet exo.
Lia07
J'ai trouvé quelques réponses. Pouvez vous me dire si c'est ça?
1. Le rayon de S est de 3 et S a pour axe l'axe (Oz) donc tout point M de S est a la distance 3 de (Oz). De même, tout point situé a la distance 3 de (Oz) est un point de S puisque le rayon de S est 3, et que S est centré sur (Oz)
2.
a/ S est un cylindre de rayon 3 centré sur l'axe (Oz) donc l'intersection de S avec un plan parallèle à (xOy) est un cercle de rayon 3.
b/ Il n'y a pas d'intersection de S avec un plan d'équation z = -4 car z  [ 0,7]
[ 0,7]
3. La je sèche toujours.
4.
a/Je vois pas trop comment faire après ça :
Merci
Bonjour ! Je dois également faire cet exercice en DM et il me pose des difficultés..Le début passe à peu près mais à partir de la question 3, ça se gâte ! Pourriez-vous m'aider ?




