Inscription / Connexion Nouveau Sujet
Sections planes d'un cylindre
 Bonjour à tous!
Bonjour à tous! 
J'ai un dm de maths spé à rendre dans 2 jours et je n'ai pas trop voir pas du tout compris! 
Alors voici l'énoncé:
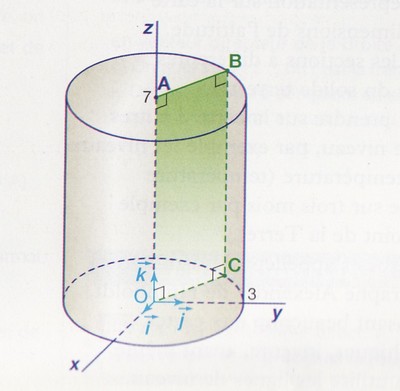
La figure ci-dessous représente le cylindre de révolution engendré par la rotation du segment [BC] autour de l'axe (Oz), le quadrilatère OABC étant un rectangle. Le point A a pour coordonnées (0, 0,7) dans le repère orthonormal (I,,,) et AB = 3. Analytiquement, le cylindre est l'ensemble des points M de l'espace dont les coordonnées (x,y, z) vérifient :
x² + y² = 9 et 0 z 7
Nous nous intéressons maintenant à l'ensemble S des points M (x,y,z) de l'espace, dont les dont les coordonnées (x,y, z) vérifient :x² + y² = 9
1. Prouvez que tout point M de S est à la distance 3 de l'axe (Oz) et réciproquement, que tout point situé à la distance 3 de l'axe (Oz) est un point de S.
2. On rappelle que le plan P d'équation z = 5 est parallèle au plan (xOy) (d'équation z=0). P est l'ensemble des points M(x,y,z) de l'espace tel que z = 5.
a) Expliquer pourquoi l'intersection de ce plan P et du cylindre S est un cercle centré sur l'axe (Oz) de rayon 3.
Je dirais que le plan P étant parallèle à (xOy), il coupe S, et donc l'intersection d'un plan et d'une sphère étant un cercle, et comme S a un rayon de 3, l'intersection de P et de S est un cercle centré sur l'axe (Oz) de rayon 3.
b) Quelle est l'intersection de S avec le plan d'équation z=-4 ?
Je pense qu'il y en a pas car z [0, 7].
3. M () est un point de S et un réel quelconque
a) Que pouvez vous déduire du point N de coordonnées ( + ) ?
b) Déduisez-en qu'il existe des droites contenus dans la surface S.
4. a)Quelle est l'intersection de la surface S avec le plan d'équation x=0 ?
b) Quelle est l'intersection de la surface S avec le plan d'équation y=0 ?
c) Quelle est l'intersection de la surface S avec le plan d'équation x=1 ?
d) Plus généralement, quelle est l'intersection du cylindre d'équation x² + y² = r² avec le plan d'équation x =a ? Avec le plan y = b ? Que se passe t il pour a = r ? pour b = r?
Surface de S et S c'est pareil?
Merci à ceux qui auront la gentillesse de m'aider!!
"Nous nous interessons maintenant à l'ensemble S des points M(x,y,z) dont les coordonées (x,y,z) vérifient x²+y²=9"
C'est la phrase clé, pas besoin de tenir compte du charabia avant...
1)
S est le cylindre illimité d'axe (Oz) d'équation x²+y²=9
Le rayon du cylindre vaut  9=3
9=3
=> l'ensemble des points M(x,y,z) de l'espace est à la distance R=3 de l'axe (Oz)
Réciproquement, tout point M à la distance 3 de l'axe (Oz) appartient à S car S est le cylindre illimité d'axe (Oz) et de rayon R=3
2)a.
P : z=5 le plan parallèle à (xOy)
S le cylindre illimité d'axe (Oz) d'équation x²+y²=9
P S est le cercle définit par x²+y²=9 et z=5. Ce cercle est bien centré sur (Oz) et de rayon
S est le cercle définit par x²+y²=9 et z=5. Ce cercle est bien centré sur (Oz) et de rayon  9=3
9=3
2)b.
P : z=-4 , le plan parallèle à (xOy)
P S est le cerlce définit par x²+y²=9 et z=-4. C'est donc le cercle de centre
S est le cerlce définit par x²+y²=9 et z=-4. C'est donc le cercle de centre  (0;0;-4) de rayon 3 inclu dans P: z=-4
(0;0;-4) de rayon 3 inclu dans P: z=-4
3)a.
Un point appartient à S  ses coordonnées vérifient x²+y²0=9 , avec z quelconque
ses coordonnées vérifient x²+y²0=9 , avec z quelconque
Or M S, on en déduit que x0 et y0 vérifient x²0+y²0=9 , et cela quelque soit la valeur de z0
S, on en déduit que x0 et y0 vérifient x²0+y²0=9 , et cela quelque soit la valeur de z0
Donc N de coordoonées (x0;y0;z0+ ) appartient aux cylindre S quelque soit lambda
) appartient aux cylindre S quelque soit lambda 
 et la valeur de z0
et la valeur de z0
3)b.
Soit C le cercle de centre O et de rayon 3 dans le plan (xOy). Il existe des droites d parallèles à (Oz) passant par C engendrant le cylindre S (car S est le cylindre illimité d'axe (Oz) et d'équation x²+y²=9). Les droites qui engendrent S sont "contenues" dans la surface S
4)a.
Soit P1 : x=0 , le plan parallèle à (yOz)
P1 S : x²+y²=9 , x=0 , z
S : x²+y²=9 , x=0 , z 
 (mettre avec accolade)
(mettre avec accolade)
 y²= 9 , x=0 , z
y²= 9 , x=0 , z 

 y=3 , x=0 , z
y=3 , x=0 , z

ou y=-3 , x=0 , z

P1 S = D1
S = D1 D2, deux droites parallèles à (Oz) tel que
D2, deux droites parallèles à (Oz) tel que
D1 : (accolade) x=0 , y=3 , z

D2 : (accolade) x=0 , y=-3 , z

4)b. (plus rapide comme on a détaillé la 4)a, on applique directement le théorème)
Soit P2 : y=0 , le plan parallèle à (xOz)
-3 0
0 3
3
Donc P2 S = D1
S = D1 D2 avec
D2 avec
D1 : (accolade) x =  (R²-0²) , y=0 , z
(R²-0²) , y=0 , z 

D2 : (accolade) x = - .... idem juste le moins devant la racine
.... idem juste le moins devant la racine
 D1 : (accolade) x=3 , y=0 ,z
D1 : (accolade) x=3 , y=0 ,z 

D2 : (accolade) x=-3 , ... idem
4)c.
Soit P3 : x=1, le plan parallèle à (yOz)
-3 1
1 3
3
Donc P3 S = D1
S = D1 D2 avec
D2 avec
D1 : (accolade) x=1 , y= (R²-1²) , z
(R²-1²) , z 

D2 : (accolade) x=1 , y= - (R²-1²) , idem
(R²-1²) , idem
 D1: (accolade) x=1 , y=
D1: (accolade) x=1 , y= 8 = 2
8 = 2 2 , z
2 , z 

D2 : (accolade) exactement pareil sauf - devant la racine
4)d.
De manière générale :
Soit  le cylindre d'équation x²+y²=r² , P: x=a
le cylindre d'équation x²+y²=r² , P: x=a
* si -r a
a r
r

 P = D1
P = D1 D2 avec
D2 avec
D1: (accolade) x=a , y= (r²-a²) , z
(r²-a²) , z

D2: (accolade) exactement pareil sauf - devant la racine
* si a [-r;r]
[-r;r] 
 P = accolade
P = accolade  accolade fermée
accolade fermée
* pour a=r 
 P est une droite D d'équation x=a , y=
P est une droite D d'équation x=a , y= (r²-r²) =0 , z
(r²-r²) =0 , z

Soit  le cylindre d'équation x²+y²=r², P: y=b
le cylindre d'équation x²+y²=r², P: y=b
* si -r b
b r ,
r , 
 P = D1
P = D1 D2 avec
D2 avec
D1 : (accolade) x =  (r²-b²) , y=b , z
(r²-b²) , y=b , z

D2 : idem sauf - devant la racine
* si b  [-r;r]
[-r;r] 
 S=
S=
* pour b=r 
 P = D avec D: (accolade) x=0 , y=a , z
P = D avec D: (accolade) x=0 , y=a , z

Pour la 1) il vaut mieux mettre tout point M de S au lieu de "l'ensemble des points M(x,y,z) de l'espace"
"accolade" signifie qu'il est plus clair de faire
x=0
y=3
z

que de les aligner
(ceci est un exemple)
A demain, essayez de pas recopier à la lettre 


