Inscription / Connexion Nouveau Sujet
sections planes de solides
bonjour, j'ai fait un exercice de mon dm mais je ne suis pas sure que ce soit juste.
consigne : on a caché des boîtes de conserve cylindriques sous des cônes en papier de hauteur 30cm. Chaque boîte a un rayon de base de 4.8cm et une hauteur de 12cm. Les cônes sont disposés en ligne, les uns à côtés des autres, sur une étagères de 1.5m de long. Combien de cônes peut-on placer sur l'étagère?
mon résonnement :
je calcule le coefficient : k=so'/so k=18/12=3/2
La section est une réduction de la base du cône donc un disque, dans le rapport k=so'/so soit 18/12=3/2.
On note A l'aire de la base et A' l'aire de la section, alors A'=PIxR²
=pix4.8²
=576/25 pi
=72.38cm²
soit A=1.5²x576/25pi
=1296/25pi
=162.86cm²
je sais que : A=pi fois rayon fois rayon
or : 1296/25pi=pi fois rayon fois rayon
1296/25pi diviser pi= rayon fois rayon
51.84=rayon fois rayon
racine carré de 51.84= rayon
7.2cm=rayon
sachant que le rayon est de 7.2cm, alors le diamètre est 7.2x2=14.4
je calcule le nombre de cône que l'ont peut mettre sur l'étagère : 150/14.4=10.42
donc on pourra mettre maximum 10cône sur l'étagère qui mesure 1.50m.
pouvez-vous me dire si cela est juste svp 
merci d'avance
svp, je sais que vous n'êtes pas à ma disposition, je suis sincèrement désolée mais c'est urgent, il faut juste me dire si c'est juste ou faux. :s
dsl 

Bonjour alyssa23
Et en utilisant Thalès ! !
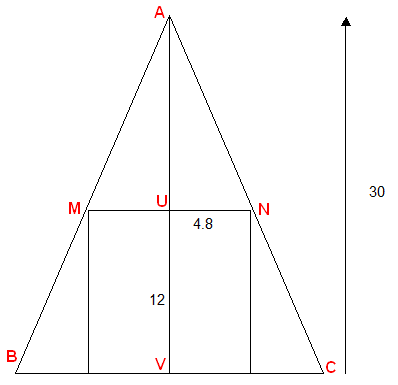
MN/BC = AU / AV
9.6/BC = 18 / 30 soit 18.BC = 9.6*30 d'où BC = 16 cm
L'étagère mesure 150 cm de long ==> 150/16 = 9 arrondi à l'unité
Combien de cônes peut-on placer sur l'étagère : 9

Non, pas forcément faux mais sûrement très compliqué et quand les choses deviennent compliquées il y a beaucoup plus de chance de faire des erreurs.
Les matheux sont des êtres fainéants (au moins ils en font au plus ils maîtrisent le sujet)
Il existe un théorème qui dit : "entre deux démonstrations ou deux théories, la meilleure est toujours la plus simple"
Un conseil de vieux crouton : Lis 5 fois un énoncé avant de te lancer, fais des schémas etc... et tout cela pour bien comprendre le problème. Quand le pb est bien compris, lance toi alors seulement dans la démonstration, les calculs, les formules et tout l'attirail nécessaire ... mais l'important reste l'intellect, l'astuce, la ruse, la méthode etc.
A+


