Inscription / Connexion Nouveau Sujet
Sections planes de surfaces
Bonjour, j'ai un dm de spé maths et je ne vois pas du tout comment faire ma deuxième partie.
Voici la 2ème partie de l'énoncé:
On note I et J les points définis par vecteur(OI)= et vecteur(OJ)=
et vecteur(OJ)= .
.
On considère alors un nouveau repère (O; ';
'; ';
'; ) tel que
) tel que  '= vecteur(OI') et
'= vecteur(OI') et  '= vecteur(OJ') où I' et J' sont les images respectives de I et J par la rotation de centre O et d'angle
'= vecteur(OJ') où I' et J' sont les images respectives de I et J par la rotation de centre O et d'angle  /6. La figure ci-dessous illustre la situation.
/6. La figure ci-dessous illustre la situation.
On note (X;Y;Z) les coordonnées d'un point de l'espace dans ce nouveau repère.
1) Compléter les égalités suivantes  '=...
'=... +...
+... et
et  '=...
'=... +...
+... .
.
2)Compléter vecteur(OM)=... +...
+... +...
+... =...
=... '+...
'+... '+...
'+... puis déduire les formules de changement de repère (donnant x,y et z en fonction de X, Y et Z)
puis déduire les formules de changement de repère (donnant x,y et z en fonction de X, Y et Z)
3) Démonterr que l'équation de ( ) [qui est 2x²+2[!!!smb]racine 3[/smb]xy+3z²=O] dans le nouveau repère est X²+Z²=1/3Y².
) [qui est 2x²+2[!!!smb]racine 3[/smb]xy+3z²=O] dans le nouveau repère est X²+Z²=1/3Y².
4) Déduire que ( ) est un cône dont on donnera les caractéristiques (on donnera en particulier son angle au sommet).
) est un cône dont on donnera les caractéristiques (on donnera en particulier son angle au sommet).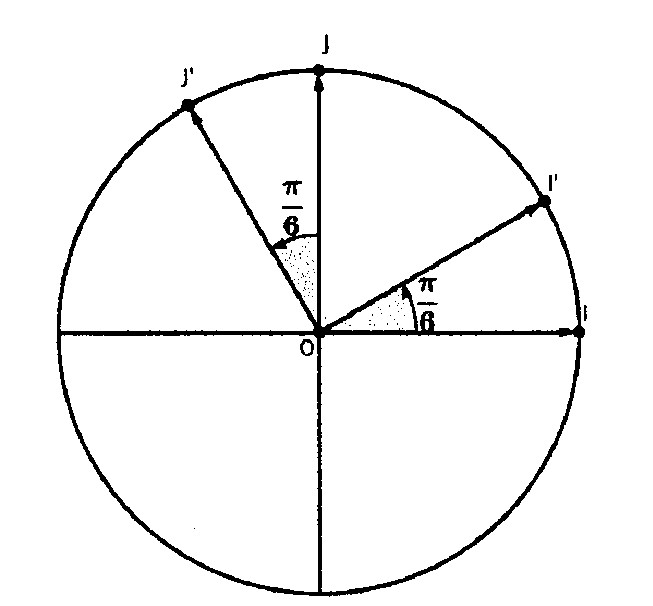
Bonjour Flora ,
je suppose que tu as écrit (en vecteurs) :
i'=OI'=OI''+I''I'= i 3/2+j/2 (1)
3/2+j/2 (1)
et j'=OJ'=OJ'''+J'''J'= j 3/2-i/2 (2)
3/2-i/2 (2)
2) OM=ix+jy+kz=i'X+j'Y+kZ ---> z=Z
on a donc ix+jy=i'X+j'Y
en remplaçant i' et j' par (1) et (2)et en identifiant les coefficients de i et j , on trouve :
x=X( 3)/2 -Y/2 , y=X/2+Y(
3)/2 -Y/2 , y=X/2+Y( 3)/2 et z=Z .
3)/2 et z=Z .
3)En remplaçant dans x , y , et z par leur expression en fonction de X,Y et Z dans 2x²+2xy 3+3z² , tu trouves l'expression de
3+3z² , tu trouves l'expression de  dans le nouveau repère .
dans le nouveau repère .
4) si on coupe cette surface par un plan // XOZ ( c'est à dire pour un Y donné) on obtient un cercle X²+Z²=Cte ---> c'est un cercle d'axe OY --- > cône de révolution .
Son sommet est X=Y=Z=0 .
Si on coupe ce cône par un plan contenant OY ,par exemple X=0 , on obtient Z²=Y²/3 il s'agit de 2 droites faisant un angle de 2 dont Tg(2
dont Tg(2 )²= 3 ... sauras- tu conclure ?
)²= 3 ... sauras- tu conclure ?
Bonne journée .