Inscription / Connexion Nouveau Sujet
Séries statistiques à 2 variables
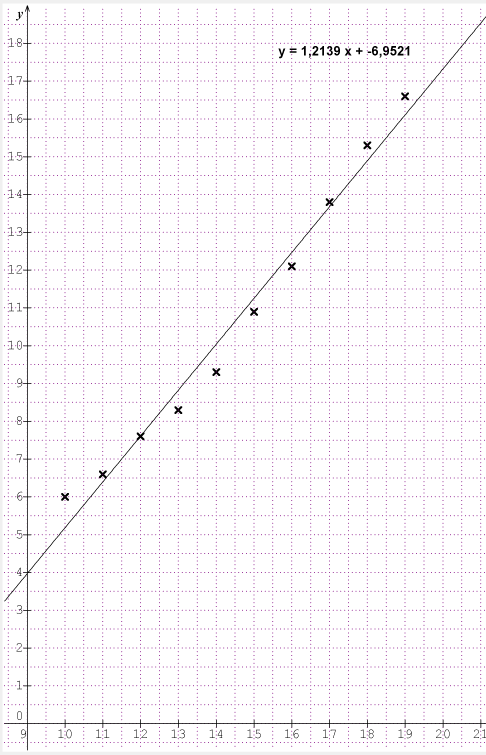
| Année | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| Rang xi | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| Capacité yi | 6 | 6,6 | 7,6 | 8,3 | 9,3 | 10,9 | 12,1 | 13,8 | 15,3 | 16,6 |
On cherche à étudier la capacité du parc éolien Français afin de savoir si, à terme, il peut être capable de supporter 50 % de l'énergie nécessaire à la recharge des véhicules électriques circulant sur le territoire.
1. Trouver l'équation de la droite (d) passant par les points correspondant aux rangs 10 et 19 de cette série de données y = 53/45 x - 52/9
2. Calculer l'erreur relative totale commise en utilisant la droite (d) comme modélisation de la série statistique.
Je vous remercie d'avance

salut
y a-t-il bien tout l'énoncé ?
tu dois bien avoir dans ton cours quelque chose qui te parle de l'erreur relative ...
Bonjour,
Avant ces deux questions j'ai représenté, dans un repère orthogonal, le nuage de points de coordonnées (xi ; yi).
Bonjour
Je pense qu'il faut calculer pour chaque valeur la différence existant entre la valeur donnée par le tableau et la valeur donnée par la droite :
exemple
on fait cela pour toutes les valeurs et on effectue la somme
Vous avez 10 points qui ont pour coordonnées et une droite d'équation
Les points de cette droite sont des estimations. En considérant l'ordonnée du point de la droite et la valeur établie, on commet une erreur. C'est icelle que l'on mesure.
On mesure la distance entre le point estimé et le point réel pour une même valeur ou abscisse. Peu nous chaut ce que représentent ces points.
L'erreur globale est donc la somme de ces erreurs.
Bonjour, je vous remercie de votre explication.
Dans la première question, on ne me demande pas d'arrondir, je laisse donc en écriture fractionnaire ?
Bonjour
À quelle occasion ? si c'est l'équation de (d) vous pouvez donner
une version fractionnaire et ensuite une valeur approchée
y = 53/45  x - 52/9
x - 52/9
y = 1,177777778  x - 5,777777778
x - 5,777777778
Comme cela ? Si oui, combien de chiffre après la virgule faut-il mettre, s'il vous plaît ?
erreur commise lors de l'année 11
erreur commise lors de l'année 12
Pourquoi arrondissez-vous le résultat pour l'erreur commise lors de l'année 12 et non pour l'année 11 ?

Dans la prochaine question, j'ai trouvé l'équation de la droite d'ajustement affine (d')  y = 1,2
y = 1,2  x - 7
x - 7
Également, on me demande de calculer l'erreur totale commise en utilisant la droite (d').
Erreur commise lors de l'année 10 : 1,2 × 10 - 7 - 6 = - 1
On considère l'erreur comme la distance entre l'ordonnée du point et celle
obtenue par la droite, c'est un nombre positif
Comme pour les premiers, il n'y avait pas de problème, je n'avais pas écrit la valeur absolue
je ne vois pas trop l'intérêt de cette question 2/ en bac techno mais pour en revenir à
On cherche à étudier la capacité du parc éolien Français afin de savoir si, à terme, il peut être capable de supporter 50 % de l'énergie nécessaire à la recharge des véhicules électriques circulant sur le territoire.
je réitère ma demande :
y a-t-il bien tout l'énoncé ?


 équivalences des systèmes de niveaux scolaires
équivalences des systèmes de niveaux scolaires


 Statistique descriptive à deux variables en terminale
Statistique descriptive à deux variables en terminale