Niveau terminale

similitude

Posté par
dykha93 29-05-12 à 21:26

bonsoir à tous j'aimerais que vous m'aidez sur cet exercice

le plan complexe est muni d'un repère orthonormal (o,,) d'unité 5 cm .soit f la transformation qui a tout point M d'affixe Z ASSOCIE LE POINT M'tel que Z'=(1/2+1/2i)Z+1
1-justifier que f est une similitude directe et préciser ses éléments caractéristiques .
2-on note A₀ le point O et pour tout n on pose A_n+1=f(A_n)
a-déterminer les affixes des points A₁,A₂,A₃ puis placer les points A₀,A₁,A₂ et A₃.
b-pour tout n on pose U_n=A_n. justifier que la suite (U_n)est une suite géométrique puis écrire U_n en fonction de n.
3-quelle est la nature du triangle A_nA_n+1

Posté par similitude 29-05-12 à 21:48

pour la première et 2-a je n'ai pas de problème
alors f est une similitude de rapport K=(2)/2
=/4
=1-i

A₀=0
A₁=1
A₂=3/2+1/2i
A₃=3/2+i

mon problème c'est comment démontrer que Un est une suite géométrique .on m'a dit que je dois passer
                       U_n=A_n
                       U_n+1=A_n+1
donc   A_nA_n+1=KU_nU_n+1

on peut DIRE que U_n est une suite géométrique de raison q=(2)/2 ??

Posté par re : similitude 29-05-12 à 23:34

tu peux vérifier ton calcul de $\Omega$

Posté par similitude 30-05-12 à 00:29

=1/[1-(1/2+1/2i)]
                   =1/[1/2-1/2i]
                   =(1/2+1/2i)/[(1/4)+(1/4)]
                   =(1/2+1/2i)/(2/4)
                   =(1/2+1/2i)/(1/2)
donc =1+i tu as raison et pour la suite ?

Posté par re : similitude 30-05-12 à 08:29

alors maintenant que $\Omega$ , d'affixe $\omega = 1+i$ est déterminé, tu peux vérifier (c'est le cas de toutes les similitudes directes ayant un unique "point fixe" $\omega$ ) que

la transformation définie par
$z'=(\frac12+\frac12i)z+1$

peut s'écrire

$z'-\omega = \frac12(1+i)(z-\omega)$

Attention toutefois, on voit réapparaître $1+i$ en facteur de $z$ , mais ici, c'est un hasard. En général ce n'est pas le cas.

et comme $1+i=\sqrt2 e^{i\frac{\pi}4}$

$z'-\omega = \frac1{\sqrt2}e^{i\frac{\pi}4}(z-\omega)$

Interprétation géométrique de cette relation :
le point $M'$ d'affixe $z'$ s'obtient à partir du point $M$ d'affixe $z$ par les opérations suivantes (commutatives) :
- Obtention de $M_1$ par rotation de $M$ d'angle de mesure $\frac{\pi}4$ autour de $\Omega$
- Obtention de $M'$ par homothétie de rapport $\frac1{\sqrt2}$ sur $M_1$ , de centre $\Omega$

passons à la suite de complexes et de leurs points associés engendrée par l'application récursive de cette transformation à un point initial.
L'énoncé prend pour point initial l'origine du repère, O, d'affixe 0, qu'il appelle fort opportunément $z_0$

et ensuite, on calcule les complexes successifs par application de la relation
$z_{n+1}-\omega = \frac1{\sqrt2}e^{i\frac{\pi}4}(z_n-\omega)$

Les points $A_n$ d'affixes respectifs $z_n$ sont représentés sur le schéma ci-dessus par les croix rouges
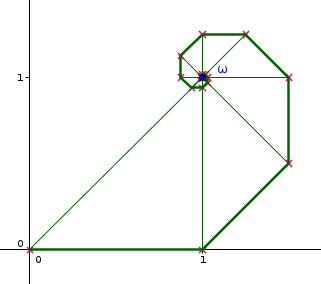
similitude
On les voit s'enrouler en spirale décroissante autour de $\Omega$

Ensuite, l'énoncé s'intéresse à la suite de réels $u_n=\Omega A_n$ que sont les longueurs des rayons, des segments joignant $\Omega$ aux points $A_n$

On a tout simplement, par application directe de la propriété du module d'un complexe :
$u_n=|z_n-\omega|$

et donc la relation de récurrence qui en découle
puisque
$z_{n+1}-\omega = \frac1{\sqrt2}e^{i\frac{\pi}4}(z_n-\omega)$
alors
$|z_{n+1}-\omega| = |\frac1{\sqrt2}e^{i\frac{\pi}4}(z_n-\omega)|$
et donc, par la propriété du produit des modules
$|z_{n+1}-\omega| = |\frac1{\sqrt2}|\times|e^{i\frac{\pi}4}|\times|z_n-\omega|$
or $|\frac1{\sqrt2}|=\frac1{\sqrt2}$ , $|e^{i\frac{\pi}4}|=1$ , $u_{n+1}=|z_{n+1}-\omega|$

et finalement
$u_{n+1}=\frac1{\sqrt2} u_n$
suite géométrique de raison $\frac1{\sqrt2}$ , raison qui est strictement dans l'intervalle $]0;1[$ , donc les termes de la suite sont toutes du même signe (remarque : il est ici positif, $u_n$ représente une distance), et tendent vers 0 quand $n\to\infty$

soit $u_0=|z_0-\omega|=|-\omega|=|\omega|=\sqrt2$

alors $u_n=\sqrt2 \left(\frac1{\sqrt2}\right)^n$

qu'on peut arranger pour écrire
$u_n=\frac1{\sqrt2^{n-1}}$

pour finir, tu sauras justifier pourquoi $\Omega A_n A_{n+1}$ est un triangle rectangle isocèle de sommet $A_{n+1}$

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

Fiches de niveau terminale
73 fiches de mathématiques en terminale disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

similitude

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths