Inscription / Connexion Nouveau Sujet
Similitude - Construction d'un point
Bonjour, j'ai un dm a faire pour demain et je suis bloqué. J'aimerais donc un peu d'aide 
Voici l'énoncé :
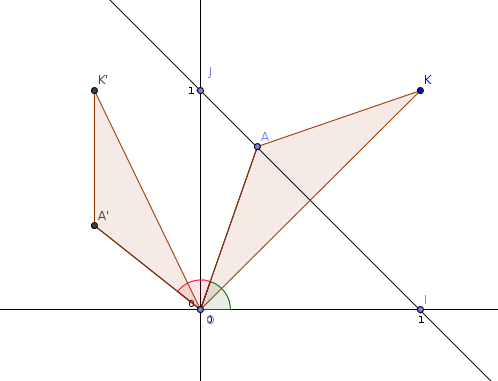
Dans le plan orienté, OIKJ désigne un carré de côté 1 tel que (OI , OJ) = Pi/2
A est un point quelconque de la droite (IJ) différent de I. s désigne la similitude directe de centre O qui transforme I en A. Les images de J, K et A par s sont respectivement notées J',K',A'.
1)a Quelles est la nature du quadrilatère OAK'J'?
b- Prouver que les points J',A et A' sont alignés?
c- Comparer les angles (OI, OA) et (OI, OA')
d-Prouver que A'O = A'K'
Merci d'avance !
1a) et 1b) les propriétés fondamentales des similitudes te permettent de répondre facilement à la question
Pour la b- il me semble avoir trouvé par contre pour les autres je ne voit pas ce que je peux utiliser :/
Ah lol. Dans mon cours la seule chose ayant un rapport avec l'alignement des points est une démonstration par l'absurde, c'est ça?
Pourquoi tu fais semblant ?
Une similitude est une transformation (ici dans le plan) qui
- conserve le rapport des distances
- conserve les angles non orientés
Une similitude directe dans le plan conserve en outre l'orientation des angles.
Est-ce qu'on te demande de faire les démonstrations en te basant sur les nombres complexes ?
Non. Et je ne fais pas semblant je pensais pouvoir m'aider de ça pour répondre à la question.
La conservation des angles orientés justifie l'alignement des points?
non
écoute, je vais t'offrir une bonne note.
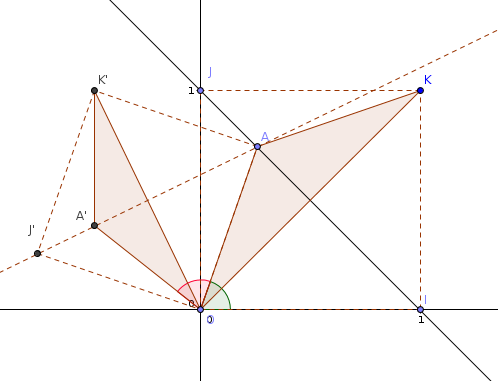
1a) OAK'J' est l'image par une similitude directe du carré OIKJ. Donc OAK'J' est un carré de même orientation que le carré initial.
1b) J', A et A' sont les images par une similitude directe des points J, I et A. Or ces trois derniers points sont alignés. Donc leurs images J', A et A' sont aussi alignées
1c) A, O et A' sont les images par une similitude directe des points I, O et A, donc les angles orientés et
sont identiques.
Donc une simple relation de Chasles nous permet d'établir que est le double de
1d) Le point A étant sur la droite (IJ) du carré OIKJ, nous avons égalité des longueurs OA=AK.
K', A' et O étant les images par une similitude directe des points K, A et O, nous avons aussi égalité des longueurs OA'=OA et A'K'=AK
nous en déduisons que OA'=A'K'


