Et si tu nous définissais S ?

enfin, si l'expression de S est exacte, rapport et angle sont corrects, mais pas le centre.

je rectifie, le centre de la SD est =1

Je dirais que A_n+1= (-i+1)z_n+i ...?

suite geometrique, A_n = A₁(1-i)ⁿ+1 ?? je trouve pas ce qu'il faut

Puisque 1 est le centre, il doit jouer un rôle particulier

étudie la suite auxiliaire t_n=z_n-1

Au fait, que vaut z₀ ?

D'après ce que je vois de ton énoncé incomplet (et je ne te félicite pas pour ça), z₀=0

ce qui donne tout son sens, finalement, à z_a et z_b

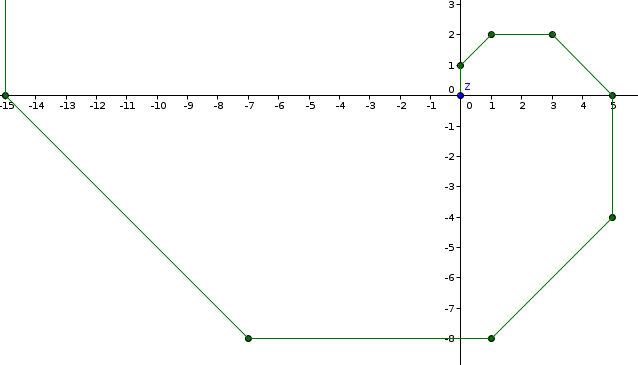
je l'ai sous entendu en disant que A₀ etait l'origine du repère...

avec t_n=z_n-1, on a: u₁=1-i, u₂=-2i, u₃=-2-2i, u₄=-4, u₅=-4-4i, u₆=8i

Cependant, je ne comprend pas d'ou vient le 1 de z_n=1-(1-i) et je n'arrive pas a ctte formule...

A_n+1=S(A_n) donc A_n+1=z_n(1-i)+i soit A_n=i(1-i)ⁿ+i ?? en divisant par i on trouve 1+(1-i)ⁿ..

Ah oui, A₀ origine du repère, ce n'était même pas sous-entendu, c'était dit et j'ai sauté l'information.


Comme tu n'avais défini S, si tu veux (et si je ne me trompe pas, mais je pense que tu aurais sauté sur l'occasion pour me le faire remarquer), et que ton centre était erroné, j'étais un peu dépité.



on pose
donc et

devient


t_n est géométrique
et comme


et puisque  



donc



Le même escargot, avec un peu plus de recul.

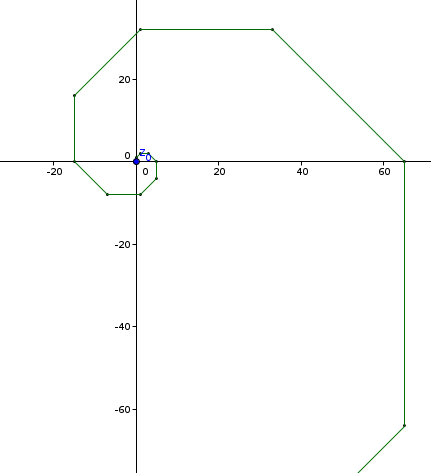
ah d'accord, en fait c'est la première fois que j'ai une suite construite avec une similitude donc j'étais un peux perdu.. Merci!!

je crois qu'il y a une faute de frappe: t_n+1+1 = (1-i)(t_n+1)+i = (1-i)t_n+1 donc t_n+1=(1-i)t_n

ça va, je suis rassuré, tu ne contentes pas de recopier. Bien.

Héhé!!

Il me reste 3 questions ou je pensais avoir bon mais...:
a) Calculez le nombre complexe (z_n+1-z_n) / (z_n-)

Je trouve -i

b) Interpretez le résultat précédent pour décrire une construction du point A_n+1 connaissant le point A_n.

On en déduite que l'angle orienté (A,A_nA_n+1) = arg(-i) = -/2 mais ça ne colle pas avec ta figure...

c) Quels sont les points de la suite (A_n) appartenant à la droite (B)? Justifier

si B est le point d'affixe z₂, tout les z_2+4K (avec k) les points coupent la droite (B) mais je ne sais pas comment justifier...

j'ai rien dit pour la b), ça colle

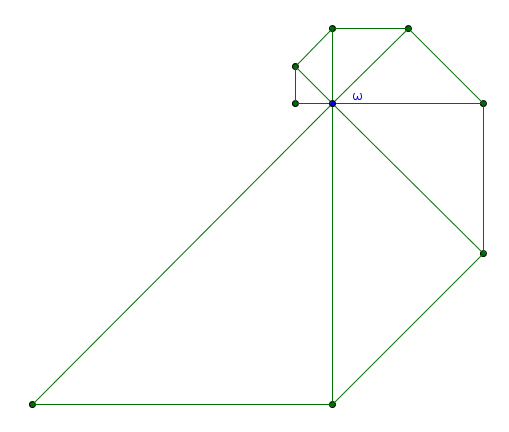
c'est exact.
donc ces deux complexes ont même module, et la différence de leur argument est équivalente à un angle droit indirect, c'est encore exact.


Géométriquement z_n+1-z_n correspond au vecteur
et zn- représente

l'argument du rapport des deux est une mesure de l'angle



Alors attention, tu as oublié un indice quand tu as écrit
On en déduit que l'angle orienté (A,A_nA_n+1)=-/2
il s'agit de
(A_n,A_nA_n+1)=-/2

Donc

Ce qui est plus confortable pour construire le point A_n+1 à partir du point A_n

A_n+1 est l'image par la rotation de centre A_n et d'angle +/2 de