Inscription / Connexion Nouveau Sujet
Similitude et endemble de points
Bonsoir,
j'ai une question sur les similitudes et un peu d'aide serait la bienvenue 
voici l'énoncé:
on a ABC un triangle équilateral et direct,
D symétrique de A par rapport à B et E symétrique de D par rapport à C
S similitude de rapport 1/2 d'angle -2pi/3 et telle que S(A)=B.
on demande après de construire le centre de S, oméga, et F=S(C), c'est assez simple
mais je bloque pour la suite:
on considére les points Mn définis par: M0=F et pour tout n appartenant à N, Mn+1=S(Mn)
caractériser l'application SoSoSet en déduire que l'ensemble des points des points Mn est inclus dans la réunion de trois droites que l'on précisera.
pour la caractérisation de SoSoS c'est simple, c'est une homototétie de rapport 1/8 mais je ne sais pas comment faire la déduction.
Merci 
Bonsoir,
Un dessin sur lequel sont reportés les points et
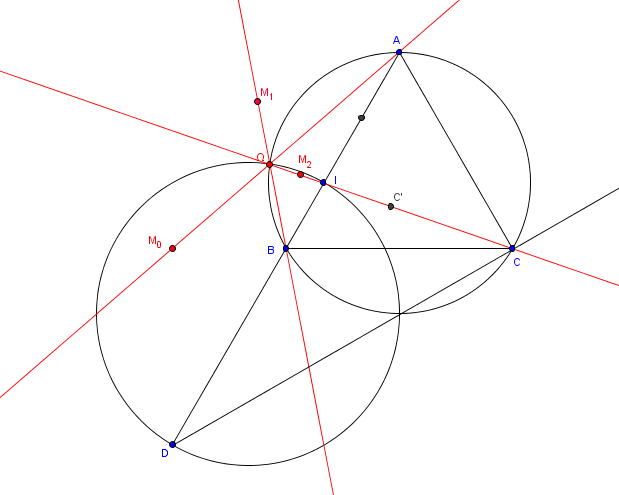
Et puisque où
est l' homothétie de centre
et de rapport
, on a

bonsoir
SoSoS est une homothétie de centre
dans cette homothétie de rapport k
M_o~>M_3~>M_6....
M_1~>M_4~>M_7~>..
M_2~>M_5~>M_8..
=k
....
les points sont donc sur la droite
de même les points sont sur la droite
et les points
sont sur la droite



