Inscription / Connexion Nouveau Sujet
similitude indirecte et complexe
bonsoir
pouvez vous m'aidez à un question svp?
voilà l'enoncée
dans le plan complexe on considere l'application h telque h(z)=z'=iz+1
1) demontrer que h est une symetrie glissante.et determiner son vecteur .
pour ce question je le démontre et j'ai trouvé que affixe du vecteur est (i+1)/2
2) donner alors une equation de l'axe (D) de h
à ce niveau je me suis bloqué aidez moi svp
et merci d'avance
Une symétrie glissante est un antidéplacement, caractérisé par un axe de symétrie orthogonale et un vecteur de translation.
avec z=x+iy, les équations cartésiennes de cette transformation sont
x'=y+1
y'=x
Je ne sais pas si ma méthode est celle que tu as vue en cours, mais tu me diras ce que tu en penses...
Pour déterminer les éléments caractéristiques, je recherche une droite globalement invariante : cette droite a une équation générale ax+by=1
et si z est sur cette droite, alors z' doit l'être aussi
x'=y+1
y'=x
ax+by=1
ax'+by'=1
En éliminant x' et y', cela donne
bx+ay=1-a
ax+by=1
et par la méthode de Gauss
(a-b)(a+b)x=a-b+ab
(a-b)(a+b)y=a-b-a²
On doit avoir une infinité de solutions, donc on doit avoir a-b+ab=a-b-a²
c'est à dire a(b+a)=0
si on choisit a=0, alors b 0, et les équations deviennent
0, et les équations deviennent
x=1/b
y=1/b
nous n'obtenons pas une droite globalement invariante. Donc a=0 est à rejeter.
si on choisit a+b=0, alors a 0 et b
0 et b 0 et les équations deviennent :
0 et les équations deviennent :
x-y=1/a
x-y=(a-1)/a
pour obtenir une droite globalement invariante, nous devons alors prendre
1/a=(a-1)/a
c'est à dire a=2
la droite globalement invariante a pour équation 2x-2y=1
le vecteur est donné alors par un point quelconque de la droite et son image.
soit z sur cette droite : ses coordonnées vérifient 2x-2y=1
et son image z' vérifie
x'=y+1
y'=x
2x'-2y'=1
le vecteur de translation a pour coordonnées (x'-x;y'-y), et on trouve (1/2;1/2)
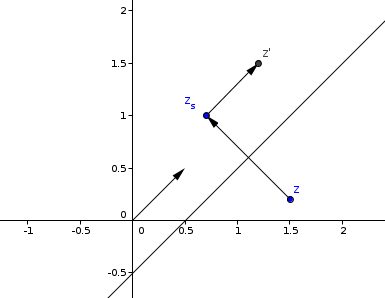
La transformation est la symétrie orthogonale par rapport à la droite d'équation 2x-2y=1 suivie de la translation de vecteur de coordonnées (1/2;1/2)
Donc tu avais trouvé le vecteur.
J'ai d'abord déterminé la droite.
bonjour
soit t la translation de vecteur (1+i)/2 et t' sa réciproque
f o t' est la réflexion d'axe (D)
On détermine l'écriture complexe de g = f o t '.
z ' = i z barre + 1/2 - i/2
Il suffit de trouver un point de (D) . On pourra cherche le point où (D) coupe l'axe des abscisses . C'est un point invariant .
z' = z ( en n'oubliant pas que z = z barre)
on peut aussi chercher les points invariants de g
z' = z avec z = x + i y .....
@ dhalte merci bien pour votre attention
votre methode est étrangère pour moi puisque dans notre cours on n'a jamais vu cette méthode de recherche d'axe et de vecteur directeur
pour moi j'ai cherché hh = t2
 où
où  est le vecteur de symetrie glissante
est le vecteur de symetrie glissante
merci bien pour votre effort et votre aide 
@ educale merci pour vous aussi votre methode me plais largement
j'ai trouvé D: x-y-1/2=0
j'espere que mon travail est juste
mercii


