Inscription / Connexion Nouveau Sujet
Similitude plane directe
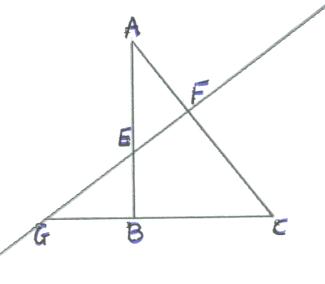
Soit ABC rectangle direct en B,
E un point de [AB],
une droite passant par E coupe [AC] en F et (BC) en G,
est le cercle circonscrit à ABC,
' est celui circonscrit à BEG,
ces 2 cercles se coupent en B et en K.
Il faut alors démontrer l'existence et l'unicité de la simlilitude plane directe S, telle que S(A)=C et S(E)=G. On déterminera l'angle de S.
J'ai cherché pendant les vacances, mais je n'y arrive vraiment pas... Si quelqu'un pouvait m'aider, ce serait génial!
Pourquoi personne ne répond? C'est trop simple? Trop compliqué?
ALOR POUR DÉMONTRER L'EXISTANCE ET L'UNICITÉ DE CETTE SIMILITUDE JE TE PROPOSE DE SUPPOSER KIL EN EXISTE PLUSIEURS ET DE DÉMONTRER K CES SIMILITUDES ONT MEME CENTRE ET MEME ANGLE.
POUR L'ANGLE DE CETTE SIMILITUDE C SIMPLE C ( AE,CG)= -pi/2
sauf etourderie de ma part...
Merci. Tu pourrais développer un peu? Je comprends le procédé, mais ça ne me paraît pas évident...
Quelqu'un pourrait répondre? Je suis toujours bloqué, et ça devient urgent. En plus, la réponse précédente était... disons assez moyenne: outre l'orthographe, c'était très vague (pas d'existence, et l'explication pour l'unicité ne m'avance pas).
c encore moi!
ca parait pas evident mais suppose au moin kil ya deux similitudes S1 et S2 qui repondent a ces conditions et noublie pas que dans tes cours taura une regle qui peu t'aider !!! a toi de le trouver et ce sera super simple pour toi si jamai ty arrive pa je vais te faire la solution au propre; du courage
Annuler
connectez vous