Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale SimilitudesTopics traitant de similitudes [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

similitudes

Posté par
AnOnYmOuS 04-01-13 à 16:07

Bonjour
Dans le plan orienté on considère 2 triangles équilatéraux directs ADB et ACE tels que: AB=AC=4 et (\vec{AB} ,\vec{AC}) \equiv \frac{\Pi}{4} [2\Pi]. On note O le milieu de [BC], J le milieu de [AE] et I le milieu de [AD].
1) Déterminer le rapport et l'angle de la similitude directe S de centre C telle que S(J)=A.
2) On pose K=S(O). Déterminer le rapport de la similitude directe S' de centre B telle que S'(A)=I.
3) Préciser S'(K).

J'ai besoin d'aide afin de répondre à la dernière question.
Merci

Posté par
cailloux Correcteurre : similitudes 04-01-13 à 16:51

Bonjour,

similitudes

Un rapide examen de la figure permet d' affirmer que S'(K)=O

Posté par
AnOnYmOuSre : similitudes 04-01-13 à 20:37

une petite question: comment montrer que K(OA)?
Merci

Posté par
cailloux Correcteurre : similitudes 04-01-13 à 22:15

Un nouveau dessin:

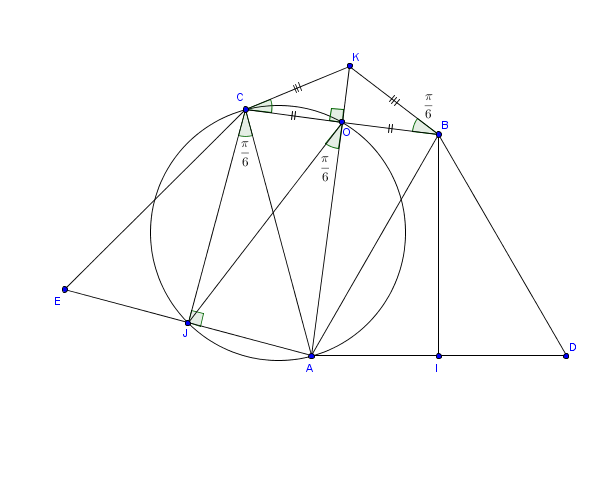
similitudes

Par exemple:

Le quadrilatère AOCJ est inscrit dans le cercle de diamètre [AC] (2 angles droit en J et O)

Donc \widehat{AOJ}=\widehat{ACJ}=\dfrac{\pi}{6}

Du coup, l' image de la droite (OJ) par S est la droite passant par S(J)=A et faisant avec elle un angle de \dfrac{\pi}{6}

C' est précisément la droite (AO) donc S(O)=K\in (AO)

Posté par
AnOnYmOuSre : similitudes 04-01-13 à 23:18

et comment montrer que l'angle KBC est égal à pi/6 ?

Posté par
cailloux Correcteurre : similitudes 04-01-13 à 23:41

Mais B est le symétrique de C par rapport à (AO) et les triangles OCK et OBK sont égaux (ou isométriques)

Posté par
AnOnYmOuSre : similitudes 04-01-13 à 23:43

je sais c'est un peu con mais comment déjà trouver la mesure de l'angle OCK?

Posté par
cailloux Correcteurre : similitudes 05-01-13 à 00:04

M' enfin, S(O)=K et S est de centre C et d'angle \dfrac{\pi}{6} alors...

Posté par
AnOnYmOuSre : similitudes 05-01-13 à 02:46



Merci

Posté par
AnOnYmOuSre : similitudes 05-01-13 à 05:44

la suite de l'exercice:
Soit R' la rotation de cantre A et d'angle /3.
Montrer que R'°S est une similitude direct.
que dois-je faire?

Posté par
AnOnYmOuSre : similitudes 05-01-13 à 13:17

aidez moi SVP

Posté par
cailloux Correcteurre : similitudes 06-01-13 à 12:11

R'\circ S est une similitude directe en tant que composée de 2 similitudes directes.

Posté par
AnOnYmOuSre : similitudes 06-01-13 à 12:52

Merci
b- Déterminer R'°S(C) et R'°S(J)
c- En déduire une construction du centre H de R'°S

b- E
A
c- je ne sais pas comment y répondre

Posté par
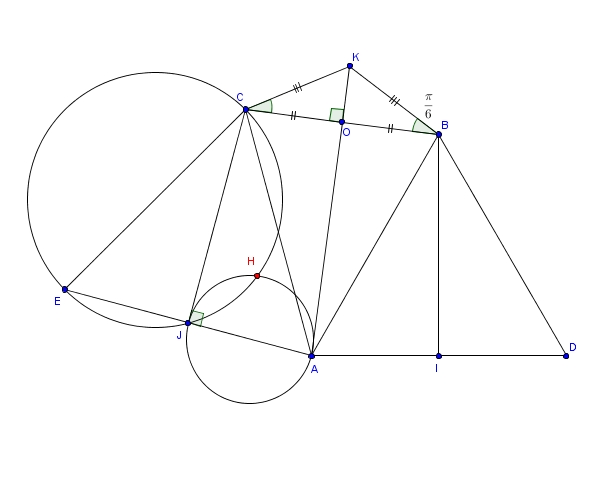
cailloux Correcteurre : similitudes 06-01-13 à 13:45

On sait donc que R'\circ S est une similitude directe.

Son angle est la somme des angles de R' et S soit \dfrac{\pi}{2}

De plus:

(R'\circ S)(C)=E donc (\vec{HC};\vec{HE})=\dfrac{\pi}{2}\;\;[2\pi] et H appartient au cercle de diamètre [CE]

(R'\circ S)(J)=A donc (\vec{HJ};\vec{HA})=\dfrac{\pi}{2}\;\;[2\pi] et H appartient au cercle de diamètre [JA]

D' où la construction:

similitudes

Posté par
AnOnYmOuSre : similitudes 06-01-13 à 13:55

merci

Posté par
cailloux Correcteurre : similitudes 06-01-13 à 13:58


Rechercher
Menu
Espace membre
11 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1742 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !